Chapter 3 Mechanistic modeling of cancer: from complex disease to systems biology
"How remarkable is life? The answer is: very. Those of us who deal in networks of chemical reactions know of nothing like it... How could a chemical sludge become a rose, even with billions of years to try."
George Whitesides (The improbability of life, 2012)
The previous chapter identified the need to organize cancer knowledge and data. The integration of biological knowledge, particularly in the form of networks, is a first step in this direction. The deepening of knowledge, however, requires the ability to manipulate objects even more, to experiment, to dissect their behaviour in an infinite number of situations, such as the astronomer with his orrery or physicians with their old anatomical models (Figure 3.1). Is it then possible to create mechanistic models of cancer in the same way?
Figure 3.1: Dissecting a biological phenomenon using a non-computational model. Rembrandt, The Anatomy Lesson of Dr Nicolaes Tulp, 1634, oil on canvas, Mauritshuis museum, The Hague
3.1 Introducing the diversity of mechanistic models of cancer
Modeling cancer is not a new idea. And the diversity of biological phenomena involved in cancer has given rise to an equally important diversity of models and formalisms, which we seek here to give a brief overview in order to better identify the specific models that we will focus on later. One way to order this diversity is to consider the scales of these models (Figure 3.2). Indeed, cancer can be read at different levels, from the molecular level of DNA and proteins, to the cellular level, to the level of tissues and organisms (Anderson and Quaranta 2008). Models have been proposed at all these scales, using different formalisms (Bellomo, Li, and Maini 2008) and answering different questions.
Consistent with the evolution of knowledge and data, the early models were at the macroscopic level. While methods and terminologies may have changed, there are nevertheless traces of these models as early as the 1950s. We then speak rather of mathematical modeling with a meaning that is intermediate between what we have defined as mechanistic models and statistical models (Byrne 2010). First, the initiation of tumorigenesis was theorized with biologically-supported mathematical expressions in order to make sense of cancer incidence statistics (Armitage and Doll 1954; Knudson 1971). These models, however, remained relatively descriptive in that they did not shed any particular light on the biological mechanisms involved and focused on gross characteristics of tumors. The integration of more advanced knowledge as well as the progressive refinement of mathematical formalisms has nevertheless allowed these models to proliferate while gaining in interpretability, with for instance mechanistic models of metastatic relapse (Nicolò et al. 2020). Always on a macroscopic scale, the study of tumor growth has also been the playground of many mathematicians (Araujo and McElwain 2004; Byrne 2010), even predicting invasion or response to surgical treatments using spatial modeling (Swanson et al. 2003). This line of research is still quite active today and provides a mathematical basis for comparison with tumor experimental growth (Benzekry et al. 2014).
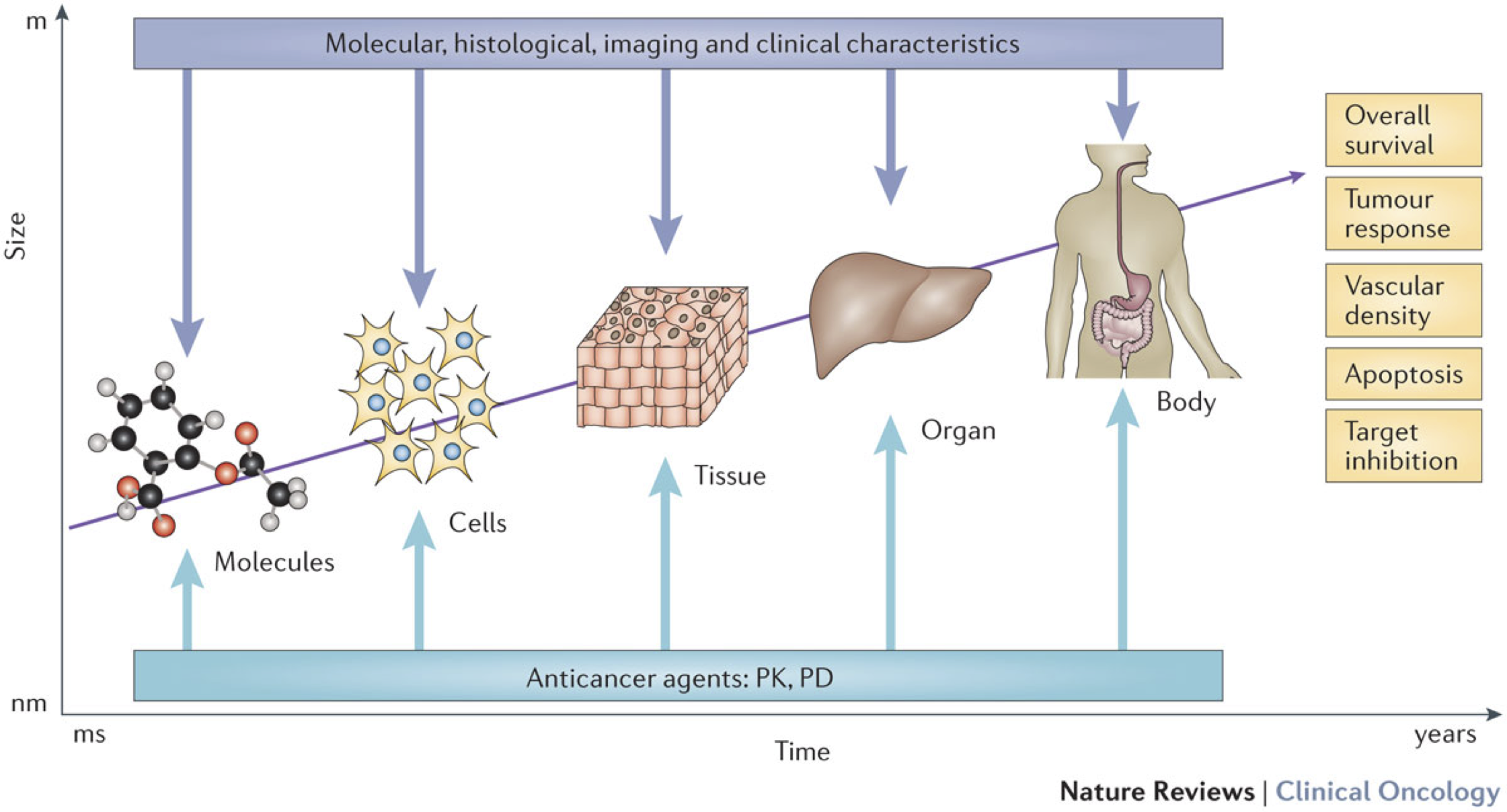
Figure 3.2: The different scales of cancer modeling. Cancer can be approached at different scales, from molecules to organs, using different data (dark blue), but often with the direct or indirect objective of contributing to the study of clinically interpretable phenomena (yellow boxes), in particular by studying the influence of anticancer agents (pale blue). Reprinted from Barbolosi et al. (2016).
Taking it down a step further, it is also possible to model cancer at the cellular level, for example by looking at the clonal evolution of cancer (Altrock, Liu, and Michor 2015). The aim is then to understand the impact of the processes of mutation, selection, expansion and cohabitation of different populations of cells, at specifc rates. The accumulation of a mutation in a population of cells can thus be studied (Bozic et al. 2010). Modeling at the cellular level is well suited to the study of interactions between cells, between cancer cells and their environment or with the immune system. Similar to other kinds of studies of population dynamics, formalisms based on differential equations are quite common (Bellomo, Li, and Maini 2008); but there are many other methods such partial differential equations or agent-based modeling (Letort et al. 2019).
Finally, at an even smaller scale, it is possible to model the molecular networks at work in cells (Le Novere 2015). The aim is then to simulate mathematically how the different genes and molecules regulate each other, transmit information and, in the case of cancer, end up being deregulated (Calzone et al. 2010). These models will be the subject of the thesis and will therefore be defined more precisely and used to detail the concepts and tools of systems biology in the following sections. It can already be noted that while these models can integrate the most fundamental biological mechanisms of living organisms, one of the most burning questions is whether it is possible to link them to the larger scales that are clinically more interesting (tissues, organs etc.). Can these models tell us something about the molecular nature of cancer? About patient survival? Their response to treatment? These questions apply to all of the above models, whatever their scales (Figure 3.2), but are more difficult to answer for models defined at molecular scale that are further from the clinical data of interest. The aim of this thesis is to provide potential answers to these questions. One of the ways of approaching these issues has been to propose multi-scale models, which are nevertheless very complex (Anderson and Quaranta 2008; Powathil, Swat, and Chaplain 2015). We will focus here on the use of models defined almost exclusively at the molecular scale, which is assumed to be prominent, to study what can be inferred on the larger scales.
Before restricting the landscape to the molecular level, it is important to point out that the diversity of mechanistic models also extends to the numerous mathematical formalisms encountered. Altrock, Liu, and Michor (2015) delivers a relatively exhaustive list of these, focusing on modeling at the scale of cell populations. For example, it includes ordinary or partial differential equations, particularly for modeling cell populations, tumor volumes, diffusion or concentration equations for various entities (e.g., oxygen or growth factors). Other formalisms, called agent-based, consider the interactions between discrete entities, often cells, each of which may experience events of interest such as mutations or cell death (Wang et al. 2014). Different more or less discrete formalizations have also been applied to cancer modeling, such as Boolean logic or fuzzy logic (Le Novere 2015). Many hybrid models also combine different approaches, such as partial differential equations for a spatial diffusion reaction coupled with cell population modeling using discrete agents on a lattice (Altrock, Liu, and Michor 2015).
However, the mechanistic nature of the models does not necessarily force them to be deterministic, i.e., to deliver always the same results from the same initial conditions. Indeed, many mechanistic models are based on stochastic or probabilistic processes, which describe the evolution over time of random variables by defining event or transition probabilities. Several examples can be found in the study of the clonal evolution of cancers through branching processes that model different cell events such as mutations, division and death that result in various evolution of the cell population size (Durrett 2015; Haeno et al. 2012). These processes fall into the category of Markov processes, which can be found applied to many other examples such as the modeling of cell positions and their evolutions on a two-dimensional lattice (Anderson et al. 2006). Note that Markov processes will be used and described in more detail in section 4.2. All in all, the strong presence of stochastic approaches thus illustrates the appropriateness of their formalism for cancer modeling where many events seem intrinsically random (e.g., appearance of a mutation) or sometimes appear as such in the current state of knowledge (e.g., change of cellular status or phenotype). Understanding the very nature of these stochastic events and their influence on global behavior is thus a major objective explored by various modeling approaches (Gupta et al. 2011; Baar et al. 2016).
3.2 Cell circuitry and the need for cancer systems biology
Most biological systems, and certainly cells, fall into the category of complex systems. These are systems made up of many interacting elements. While these systems can be found in many different scientific fields, the cell as a complex system is characterized by the diversity and multifunctionality of its constituent elements (genes, proteins, small molecules, enzymes), which nevertheless contribute to organized and a priori non-chaotic behaviour (Kitano 2002). Thus, the role of a protein such as the p53 tumor suppressor can only be understood by taking into account the interplay between its relationships with transcription factors and biochemical modifications of the molecule itself (Kitano 2002). In a cell, as in any complex system, the multiplication of components and interactions can make the response or behaviour of the system unexpected or unpredictable. Non-linear responses, such as abrupt changes in the state of a system, called critical transitions, can be observed in response to a moderate change in the signal (Trefois et al. 2015). Generally speaking, it is possible to observe emergent behaviours, i.e., behaviours of the system as a whole that were not trivially deducible from the individual behaviours of its components. This has been documented, through experiments and simulations, in the study of cell signalling pathways and the resulting biological decisions (Bhalla and Iyengar 1999; Helikar et al. 2008). These considerations have thus given rise to system-level or holistic approaches that aim to integrate data and knowledge into more comprehensive representations, often called systems biology.
What is true for the cell in general is just as true for cancer in particular. Understanding the intertwining of signaling pathways is necessary to study their contributions to different cancer hallmarks, as shown in Figure 2.7. The concepts described above can thus be transposed to cancer systems biology (Hornberg et al. 2006; Kreeger and Lauffenburger 2010; Barillot et al. 2012). Indeed, it is often a question of understanding or predicting the impact of perturbations on cellular networks. Understanding how a single genetic mutation disrupts and reprograms networks, or even predicting the responses triggered by a drug on a presumably promising molecular target, makes little sense without integrated approaches. In addition, cancers are characterized by the accumulation of numerous mutations and alterations over time that must be considered concomitantly. These points of view of biologists and modelers reinforce the observation already made in the previous chapter of cancer as a network disease, as a system disease (Figure 2.8).
Finally, to conclude this general presentation, it is important to understand that while small molecular network modeling is not recent, the rise and multiplication of wide range systems biology approaches is very much related to the production of biological data (De Jong 2002). The last few decades have seen the emergence of high-throughput data that has made it possible to identify and link hundreds of genes or proteins involved in cancer. Exploring the interaction and back and forth between these models and the data they use or predict is therefore of utmost importance. In addition, the now massive amount of data has also imposed mathematical or computational approaches as a central element in the management of this profusion and more and more modeling approaches are focused on data integration or inference (Fröhlich et al. 2018; Bouhaddou et al. 2018). More generally, Figure 3.3 shows that while the number of scientific articles devoted to cancer has increased drastically since the 1950s (panel A), the proportion of these same articles mentioning models, networks or computational approaches has also increased (panel B), illustrating a change in paradigms.
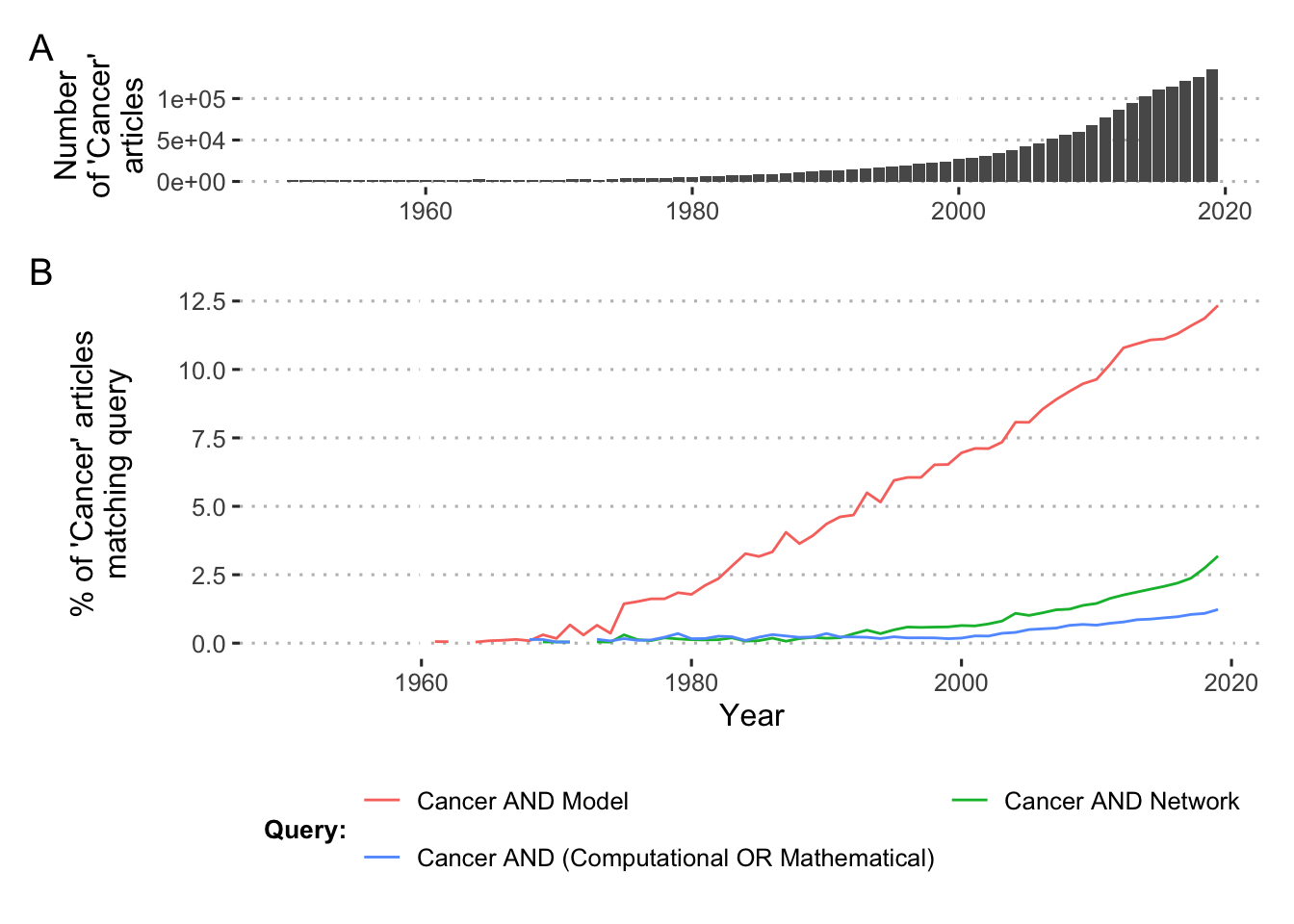
Figure 3.3: PubMed trends in cancer studies. (A) PubMed articles with the word Cancer in either title or abstract from 1950 to 2019. (B) Proportion of the Cancer articles with additional keywords expressed as PubMed logical queries.
3.3 Mechanistic models of molecular signaling
Once the context has been defined, both biologically and methodologically, it is possible to begin the exploration of the models that will constitute the core of this thesis: the mechanistic models of molecular networks and signaling pathways. Before describing and illustrating some of the existing mathematical formalisms, it is possible to describe the common fundamental elements of this family of approaches.
3.3.1 Networks and data
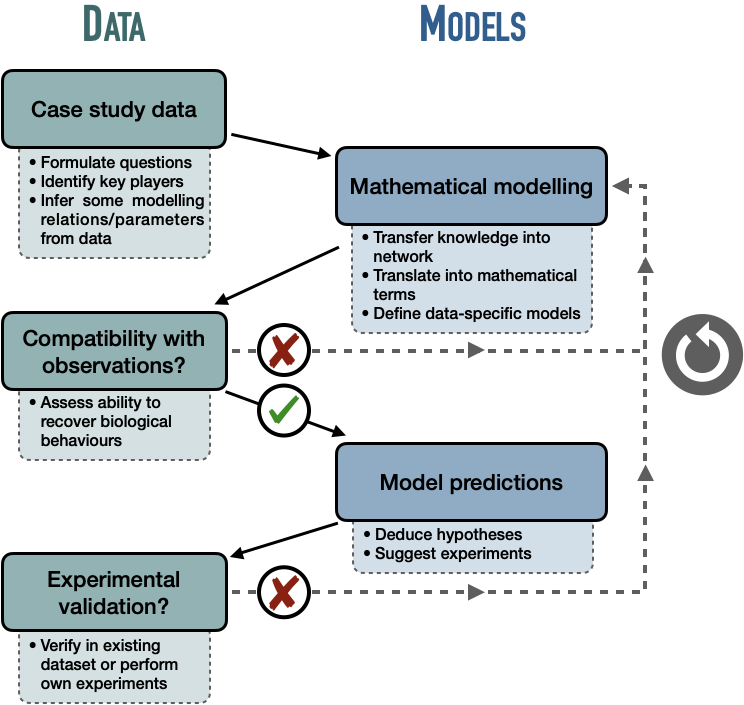
The first step is to identify the relevant biological entities from a question or system of interest (e.g. tumor suppressor genes, signaling cascades of proteins) and then to model their interactions, the regulatory relationships that link them. At this stage the model can generally be represented by a network but this word can cover different realities (Le Novere 2015). The simplest network just represents undirected interactions between entities, which therefore only establishes relationships and not causal mechanisms. But modeling requires more precise definitions, in particular concerning the direction of the interaction (is it A that acts on B or the opposite) and its nature (type of chemical reaction, activation/inhibition etc.). This is usually summarized as activity flows (or influence diagrams) with activation and inhibition arrows as in Figure 2.7 or Figure 3.5A. These arrows emphasize the transformation of static networks into dynamic objects that can be manipulated and interpreted mechanistically. This work can be taken further by writing bipartite graphs, known as process descriptions, which explicitly show the different states of each variable (first type of nodes), depending on their phosphorylation state for instance, and the reactions that link them (second type of nodes) as in Figure 3.5B. A more precise description of these different representations and their meanings can be found in Le Novere (2015). Once the network structure of the model has been defined or inferred by the modeler, it is possible to write the corresponding mathematical formalism and potentially to refine certain parameters. Finally, the model is often confronted with new data to check its consistency with the biological behaviour studied or possibly make new predictions.
However, all these steps are not linear and sequential, but rather iterative and cyclical. This modeling cycle, with back and forth to the data, is not specific to molecular network models, but it is possible to specify it in this case (Figure 3.4). The names of the key players involved in the question of interest are thus first extracted from adapted data or from the literature. A first mathematical translation of the relationships between the entities is then proposed before verifying the compatibility of this model with the observations, whether qualitative or quantitative. If the compatibility is not good, we come back to the definition or the parameterization of the model. If compatibility is correct, the model can be used to make new predictions or study phenomena that go beyond the initial data set. Ideally, these predictions will be tested afterwards. This cyclic approach with two successive checks is analogous to the use of validation and test data in the evaluation of most learning algorithms. This analogy can sometimes be masked by the qualitative nature of the predictions or by the lack of explicit fitting of the parameters.
3.3.2 Different formalisms for different applications
Beyond these similarities in the construction and representation of models, the precise mathematical formalism that underlies them varies according to the type of question and the data (De Jong 2002). For the sake of simplicity, and without exhaustiveness, we propose to divide into quantitative and qualitative formalisms which will be essentially illustrated respectively by ordinary differential equation (ODE) models and logical (or Boolean) models for which a graphical and schematic comparison is proposed in Figure 3.5.
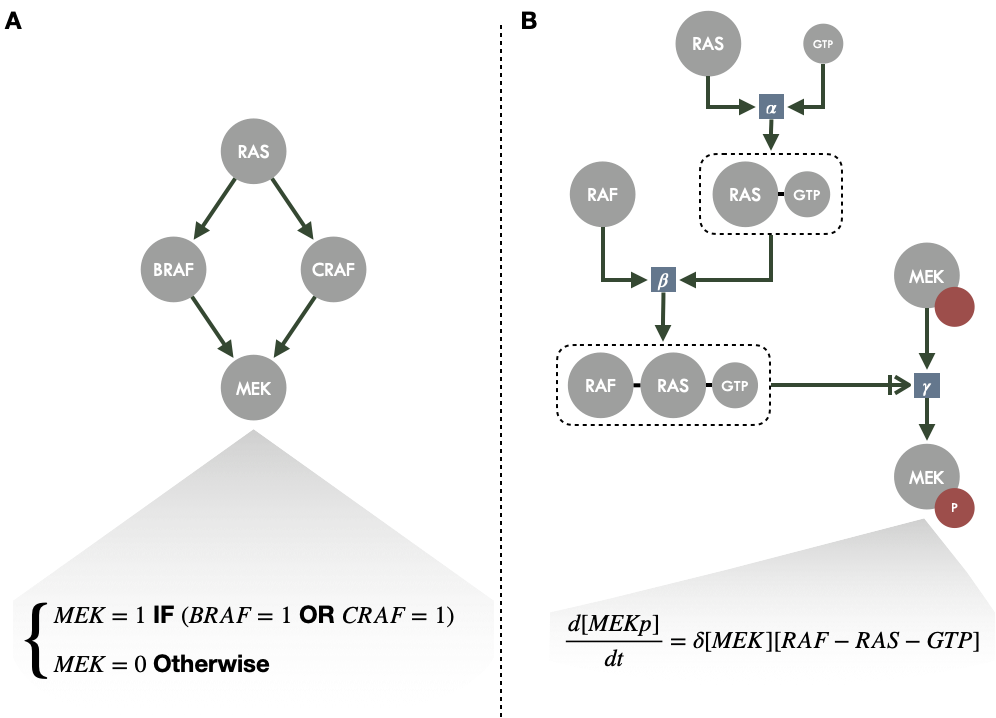
Figure 3.5: Schematic example of logical and ODE modeling around MAPK signaling. (A) Activity flow diagram of a small part of MAPK signaling, each node representing a gene or protein, with an example of logical rule for MEK node for the corresponding logical model. (B) Process description of the same diagram with BRAF and CRAF merged in RAF for the sake of simplicity; each square representing a reaction and the corresponding rate; an example differential equation is provided for the phosphorylated (active) form of MEK.
One of the most frequent approaches is the use of chemical kinetics equations to construct ODE systems which are a fairly natural translation of the process descritption networks described in the previous section (Polynikis, Hogan, and Bernardo 2009). For instance, each biological interaction can be treated as a reaction governed by the law of mass action and, under certain hypotheses, as a differential equation (Figure 3.5B); the set of reactions in the system then generates a set of differential equations with coupled variables, in an analogous way to the Lotka Volterra system presented in section 1.2.2. Thus the variables generally represent quantities of molecular species, for example concentrations of RNA or proteins, and the stoichiometric coefficients and reaction rates are used to define the system parameters. Approximations are sometimes made to simplify the equations, for example by assuming that they can be written as Michaelis-Menten's enzymatic reactions, which have a simple and well known behaviour. However, the theoretical accuracy of quantitative models has a cost since each differential equation requires parameters, such as reaction constants or initial conditions, to which the system is very sensitive (Le Novere 2015). The biochemical interpretation of the parameters sometimes allows to find their value in the literature, or in dedicated databeses (Wittig et al. 2012), if the reactions are well characterized, even if possible variations in a given biological or physical context are often unknown. Since knowledge of the values of these parameters is often limited or even non-existent, it may require a very large volume of data (including time series) to fit the many missing parameters which can be difficult if the number of parameters is large (Villaverde and Banga 2014). However, recent work has demonstrated the feasibility and scalability of this type of inference with sufficiently rich data (Fröhlich et al. 2018).
At the same time, more qualitative approaches to modeling biological networks have been proposed with discrete variables linked together by rules expressed as logical statements (Abou-Jaoudé et al. 2016). These models are both more abstract since variables do not have a direct biological interpretation (e.g. concentration of a species) but are more versatile since they can unify different biological realities under the same formalism (e.g. activation of a gene or phosphorlation of a protein). The discrete nature of the variables can then be seen as an asymptotic case of the sigmoidal (e.g. Hill function) relationships often found in biology (Le Novere 2015). The step function thus obtained can keep a natural interpretation in the context of biological phenomena: genes activated or not, protein present or absent etc. Similarly, interactions between species are not quantified but are based on qualitative statements (e.g. A will be active if B and C are active), drastically reducing the number of parameters (Figure 3.5A). If the theoretical interest of this formalism to study biological mechanisms was proposed quite early (Kauffman 1969; Thomas 1973), many concrete applications have also been developed over the years, particularly in cancer research (Saez-Rodriguez, Alexopoulos, et al. 2011a; Remy et al. 2015). This logical formalism will constitute the core of the work presented in Part II, where it will therefore be discussed in greater detail.
| Quantitative modeling | Qualitative modeling | |
|---|---|---|
| Example formalism | Ordinary differential equation (ODE) models | Logical models |
| Type of variables | Direct translation of biological quantities, usually continuous | Abstract representation of activity levels, usually discrete |
| Objective | Quantitatively accurate and temporal simulation of an experimental phenomenon | Coarse-grained simulation of qualitative phenotypes |
| Advantages | Direct confrontation with experimental data; precise; linear representation of time | Faster design; easy translation of literature-based assertions; simulation of perturbations |
| Drawbacks | Difficulty determining or fitting parameters | More difficult to link to data; lower precision |
These two formalisms, which are among the most frequent for modeling biological networks, share many similarities, in particular the propensity to be built according to bottom-up strategies based on knowledge of the elementary parts of the model, i.e., biological entities and reactions. However, they differ in their implementation and objectives, one aiming at the most accurate representation possible, the other seeking to capture the essence of the system's dynamics in a parsimonious way (Table 3.1). The opposition is not irrevocable, as illustrated by the numerous hybrid formalisms that lie within the spectrum delimited by these two extremes such as fuzzy logic or discrete-time differential equations (Aldridge et al. 2009; Le Novere 2015; Calzone, Barillot, and Zinovyev 2018). To conclude, a comparison between the two approaches applied to the same problem is proposed by Calzone, Barillot, and Zinovyev (2018), studying the epithelio-mesenchymal transition (EMT, a biological process involved in cancer), to illustrate in concrete terms their complementarity.
3.3.3 Some examples of complex features
With the help of these models, both qualitative and quantitative, many complex behaviours have been identified. Benefiting from the knowledge accumulated in the study of dynamic systems, a whole zoo of patterns with complex and non-intuitive behaviours such as non-linearities have been highlighted (Tyson, Chen, and Novak 2003). The MAPK pathway, coarsely described in Figure 3.5, and often simplified as a rather unidirectional cascade, shows switch or bistability behaviors generated by the complexity of its multiple phosphorylation sites (Markevich, Hoek, and Kholodenko 2004). These models have also been put at the service of understanding cancer and the erroneous decision-making by cells resulting from impaired signaling pathways. Thus, Tyson et al. (2011) summarize superbly well the complexity that can be hidden in the dynamics of smallest molecular networks as soon as they contain more than two entites and crossed regulations or feedback loops. Logical models have also made it possible to better dissect some complex phenomena at play in the cell such as emergent behaviours (Helikar et al. 2008) or mechanisms behind mutation patterns in cancer (Remy et al. 2015).
3.4 From mechanistic models to clinical impact?
Mechanistic models have therefore undeniably led to a better understanding of the complex molecular machinery of signalling pathways. But beyond the interest that this understanding represents, do these models also have a clinical utility? In other words, are they of clinical or only scientific value?
3.4.1 A new class of biomarkers
Throughout this thesis, the clinical value of mechanistic models will often be analyzed by analogy to that of biomarkers. Biomarkers are usually defined as measurable indicators of patient status or disease progression, such as prostate-specific antigen (PSA) for prostate cancer screening or BRCA1 mutation for breast cancer risk (Henry and Hayes 2012). Biomarkers also encompass multivariate signatures that identify more complex patterns with clinical significance. Taking the logic even further, it was therefore proposed that mechanistic models, which also reveal complex molecular behaviours, could be considered as biomarkers, capturing perhaps even dynamic information (Fey et al. 2015).
Like oncology biomarkers, the models will be divided into two categories according to their clinical objectives: prognostic models and predictive models (Oldenhuis et al. 2008). Prognostic biomarkers and models are those that provide information on the evolution of cancer independently of treatment. They are therefore generally confronted with survival or relapse data. The protein Ki-67 for example, encoded by the MKI67 gene, is known to be indicative of the level of proliferation and high levels of expression are thus associated with a poorer prognosis in many cancers (Sawyers 2008). Predictive biomarkers and models, on the other hand, give an indication of the effect of a therapeutic strategy. The simplest example, but not the only one, concerns biomarkers that are themselves the target of treatment: treatments based on monoclonal antibodies directed against HER2 receptors in breast cancer are only effective if the HER2 receptor has been detected in the patient (Sawyers 2008). Without attempting to be exhaustive, some logical and ODE models, with either prognostic or predictive claims, will be described.
3.4.2 Prognostic models
One of the first mechanistic models of cell signalling to have been explicitly presented as a prognostic biomarker is the one proposed by Fey et al. (2015) and describing c-Jun N-terminal kinase (JNK) pathway in neuroblastoma cells. A summary of the study is provided in Figure 3.6. The model is an ODE translation of the process description network of Figure 3.6A, further determined and calibrated with molecular biology experimental data obtained using neuroblastoma cell lines. We thus observe the non-linear switch-like dynamics of JNK activation as a function of cellular stress (Figure 3.6B). The precise characteristics of this sigmoidal response can, however, vary from one individual to another as captured by the network output descriptors \(A\), \(K_{50}\) and \(H\). Fey et al. proposed to perform neuroblastoma patient–specific simulations of the model, using patient gene expressions for ZAK, MKK4, MKK7, JNK and AKT genes to specify the initial conditions of the ODE system. Since JNK activation induces cell death through apoptosis, the patient-specific \(A\), \(K_{50}\) and \(H\) derived from patient-specifc models are then analyzed as prognostic biomarkers (Figure 3.6C). Readers are invited to refer to the original article for details on model calibration or binarization of network descriptors (Fey et al. 2015). The authors also showed that in the absence of positive feedback from \(JNK^{**}\) to \(^PMKK7\), an important component of non-linearity, the prognostic value is drastically decreased. All in all, this pipeline from ODE model to survival curves, thus provides a paradigmatic example of the clinical interpretation of mechanistic models of molecular networks that will be reused in later chapters for illustration purposes. Other ODE models following a similar rationale have been proposed by the same group for colorectal cancer (Hector et al. 2012; Salvucci et al. 2017) or glioblastoma (Murphy et al. 2013; Salvucci, Zakaria, et al. 2019). Machine learning approaches have also been proposed to ease the clinical implementation of this kind of prognostic models by dealing with the potential lack of patient data needed to personalize them (Salvucci, Rahman, et al. 2019).
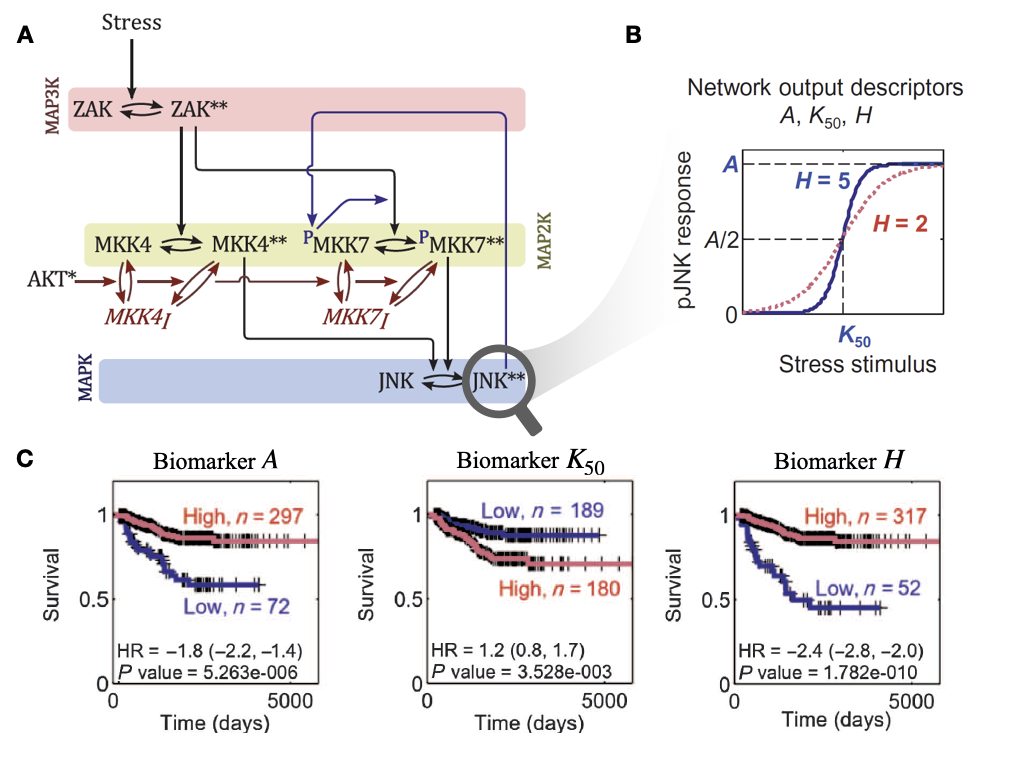
Figure 3.6: Mechanistic modeling of JNK pathway and survival of neuroblastoma patients, as described by Fey et al. (2015). (A) Schematic representation, as a process description, for the ODE model of JNK pathway. (B) Response curve (phosphorylated JNK) as a function of the input stimulus (Stress) and characterization of the corresponding sigmoidal function with maximal amplitude \(A\), Hill exponent \(H\) and activation threshold \(K_{50}\). (C) Survival curves for neuroblastoma patients based on binarized \(A\), \(K_{50}\) and \(H\); binarization thresholds having been defined based on optimization screening on calibration cohort.
On the logical modeling side, there are also studies including prognostic value validation. Thus, Khan et al. (2017) proposed two logical models of epithelio-mesenchymal transition (EMT) in bladder and breast cancers. These models are inferred from prior mechanisms knowledge and data analysis with particular attention to potential feedback loops. Using these models, it is possible to study the behaviour of them for all combinations of model inputs (growth factors and receptor proteins) and derive subsequent signatures for good or bad prognosis. These signatures are later validated with cohorts of patients. In this case, the mechanistic model does not seek to capture a dynamic behavior but to facilitate and make understandable the exploration of combinations of input signals that grow exponentially with the number of inputs considered. Other formalisms, called pathway activity analysis and following the same activity flows principles (Figure 3.5A), have been analysed in the light of their prognostic value. Their greater flexibility enables the direct use of networks of several hundred or thousands of genes, such as those present in the KEGG database (Kanehisa et al. 2012). The benefit of mechanistic modeling is then to organize high-dimensional data and to facilitate the a posteriori analysis of the results.
3.4.3 Predictive models
But the explicit representation of biological entities in mechanistic models makes them particularly suitable for the study of well-defined perturbations such as drug effects. Indeed, by assuming that the mechanism of action of a drug is at least partially known, it is possible to integrate this mechanism into the model if it contains the target of the drug (Figure 3.7). One can therefore simulate the effect of one drug or even compare several. These strategies have already been implemented in a qualitative way with logical models used to explain resistance to certain treatments of breast cancer (Zañudo, Scaltriti, and Albert 2017) or even highlight the synergy of certain combinations of treatments in gastric cancer (Flobak et al. 2015). The value of these models, however, is more scientific than clinical in that they focus on a single cell line or a restricted group of cell lines. The possibility to personalize the predictions or recommendations for different molecular profiles of cell lines or patients is therefore not obvious. Still within the context of logical formalism, Knijnenburg et al. (2016) proposed a broader approach: if their model needs to be trained, it can nevertheless provide an analytical framework for several hundred cell lines, while remaining within the scope of the training data to ensure the validity of predictions.
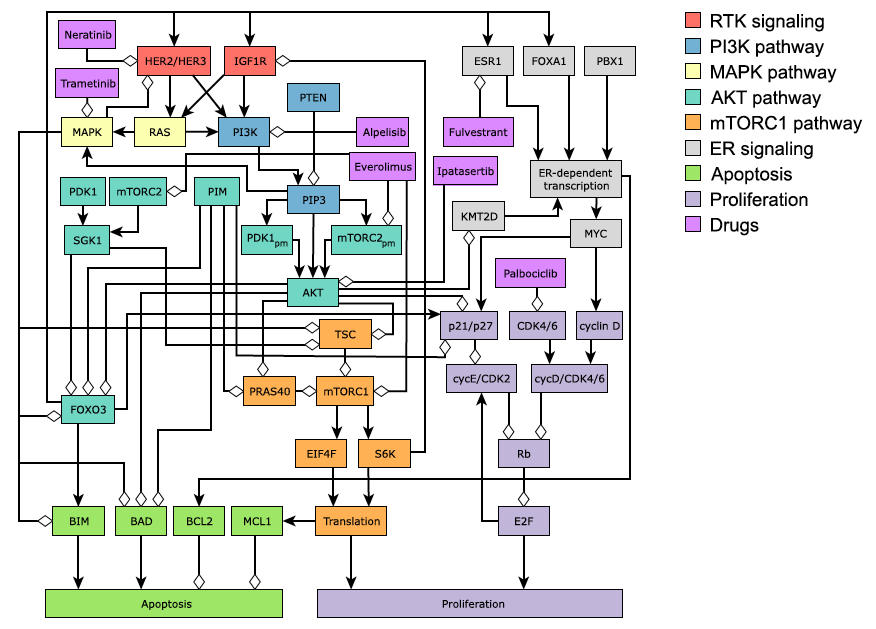
Figure 3.7: Network model of oncogenic signal transduction in ER+ breast cancer, including some drugs and their targets. Reprinted from Zañudo, Scaltriti, and Albert (2017).
Conceptually comparable strategies can be found on the side of differential equations where large mechanistic models of cell signalling are also trained to predict the response to different treatments (Bouhaddou et al. 2018; Fröhlich et al. 2018). A calibrated model can then predict the response to a combination of treatments not tested in the training data, thereby proving the ability of mechanistic models to extend their predictive value beyond the data (Fröhlich et al. 2018). As with prognostic models, mechanistic approaches other than logical formalisms and ODEs have been proposed and validated (Jastrzebski et al. 2018). What can be learned from these predictive models is that they require significant training data to be able to go beyond qualitative predictions and dissect treatment response mechanisms of many cell lines simultaneously. For obvious practical and ethical reasons, the validation of these models is for the moment limited to preclinical data since they require data for many uncertain therapeutic interventions.
3.4.4 Mechanistic models, interventions and causality
To conclude this first part in a broader way, it is interesting to note that the now complete description of mechanistic models of cancer makes it possible to revisit their characteristics from a different point of view and to link them to the statistical approaches that will be the subject of the third part of the dissertation. First of all, it should be remembered that statistical models only highlight associations between biological variables or entities and not causal relationships. On the other hand, by explicitly constraining the structure of relations between variables, mechanistic models become less flexible flexibility but already propose a causal interpretation. Therefore, the notion of causality is intrinsically embedded in the definition of the mechanistic model (section 1.2).
However, if causality is not a by-product when using a statistical or machine learning model, it is possible to access it through specific experimental designs, such as randomized clinical trials, or applying dedicated statistical methods (Hernán and Robins 2020), as described later on in chapter 8. In both cases, the aim is to compare the effect of a treatment, or more generally of an intervention, on two groups that are as similar as possible to each other in order to isolate the specific, causal effect of the intervention on outcome. Schematically, the identification of causal links can be likened to the study of well-defined interventions on patients: it is a question of being able to act in a relevant and specific way on a variable and to measure the consequences. The notion of intervention is thus very present in the literature on causality (Eberhardt and Scheines 2007) and was summarized by Holland (1986) in a concise manner: "no causation without manipulation".
In this respect, without being part of the same statistical framework at all, mechanistic models offer an interesting parallel. As suggested in the previous paragraph, they allow us to test the effect of certain interventions: how does the model behave with or without the addition of a drug to its structure? This ability to study the effect of targeted interventions again contributes, in a slightly different way, to the understanding of the system. The particularity of mechanistic models, once they have been validated, is that they can study the effect of interventions for which no data are available. In any case, a common point between the mechanistic approaches of the second part of the thesis and the statistical approaches of causal inference of the third part is to question the mechanisms and true causes at work throughout the cancer modeling process, from the biological question to clinical validation. It is indeed at this price that one can reach the level of understanding and confidence required for a real world application.
This first bridge between mechanistic models of cell signalling and clinical applications concludes this introductory part. The next part will be devoted to the definition of new methods to establish this connection based on logical formalism, before the third part proposes a more statistical evaluation of the prognostic and predictive values of the models presented in the previous parts.
Summary
The biological knowledge gathered on cancer enables to propose mechanistic models at different scales. This thesis focuses on the molecular level in a bottom-up approach based on the biochemical behaviors described in the literature. These models have in common the mathematical translation of the activation and inhibition networks that link all biological entities within a cancer cell. Different mathematical formalisms exist, including differential equations (continuous and quantitative models) and logical methods (discrete and qualitative models) which are among the most frequent and will be used as examples. For these formalisms as for the others, stochastic approaches are often proposed to translate tumor mechanisms. Most of these mechanistic models have a purely theoretical or investigative purpose but some are used to predict the evolution or response to cancer treatment, they are then respectively prognostic or predictive.
References
Abou-Jaoudé, Wassim, Pauline Traynard, Pedro T Monteiro, Julio Saez-Rodriguez, Tomáš Helikar, Denis Thieffry, and Claudine Chaouiya. 2016. “Logical Modeling and Dynamical Analysis of Cellular Networks.” Frontiers in Genetics 7. Frontiers: 94.
Aldridge, Bree B, Julio Saez-Rodriguez, Jeremy L Muhlich, Peter K Sorger, and Douglas A Lauffenburger. 2009. “Fuzzy Logic Analysis of Kinase Pathway Crosstalk in Tnf/Egf/Insulin-Induced Signaling.” PLoS Comput Biol 5 (4). Public Library of Science: e1000340.
Altrock, Philipp M, Lin L Liu, and Franziska Michor. 2015. “The Mathematics of Cancer: Integrating Quantitative Models.” Nature Reviews Cancer 15 (12). Nature Publishing Group: 730–45.
Anderson, Alexander RA, and Vito Quaranta. 2008. “Integrative Mathematical Oncology.” Nature Reviews Cancer 8 (3). Nature Publishing Group: 227–34.
Anderson, Alexander RA, Alissa M Weaver, Peter T Cummings, and Vito Quaranta. 2006. “Tumor Morphology and Phenotypic Evolution Driven by Selective Pressure from the Microenvironment.” Cell 127 (5). Elsevier: 905–15.
Araujo, Robyn P, and DL Sean McElwain. 2004. “A History of the Study of Solid Tumour Growth: The Contribution of Mathematical Modelling.” Bulletin of Mathematical Biology 66 (5). Elsevier: 1039–91.
Armitage, Peter, and Richard Doll. 1954. “The Age Distribution of Cancer and a Multi-Stage Theory of Carcinogenesis.” British Journal of Cancer 8 (1). Nature Publishing Group: 1.
Baar, Martina, Loren Coquille, Hannah Mayer, Michael Hölzel, Meri Rogava, Thomas Tüting, and Anton Bovier. 2016. “A Stochastic Model for Immunotherapy of Cancer.” Scientific Reports 6. Nature Publishing Group: 24169.
Barbolosi, Dominique, Joseph Ciccolini, Bruno Lacarelle, Fabrice Barlési, and Nicolas André. 2016. “Computational Oncology—mathematical Modelling of Drug Regimens for Precision Medicine.” Nature Reviews Clinical Oncology 13 (4). Nature Publishing Group: 242.
Barillot, Emmanuel, Laurence Calzone, Philippe Hupe, Jean-Philippe Vert, and Andrei Zinovyev. 2012. Computational Systems Biology of Cancer. CRC Press.
Bellomo, Nicola, NK Li, and Ph K Maini. 2008. “On the Foundations of Cancer Modelling: Selected Topics, Speculations, and Perspectives.” Mathematical Models and Methods in Applied Sciences 18 (04). World Scientific: 593–646.
Benzekry, Sébastien, Clare Lamont, Afshin Beheshti, Amanda Tracz, John ML Ebos, Lynn Hlatky, and Philip Hahnfeldt. 2014. “Classical Mathematical Models for Description and Prediction of Experimental Tumor Growth.” PLoS Comput Biol 10 (8). Public Library of Science: e1003800.
Béal, Jonas, Elizabeth Rémy, and Laurence Calzone. 2020. “Modélisation Logique et Données Omiques : De La Construction Des Modèles à La Médecine Personnalisée.” In Approche Symbolique de La Modélisation et de L’analyse Des Systèmes Biologiques, edited by Elisabeth Rémy and Cédric Lhoussaine. ISTE.
Bhalla, Upinder S, and Ravi Iyengar. 1999. “Emergent Properties of Networks of Biological Signaling Pathways.” Science 283 (5400). American Association for the Advancement of Science: 381–87.
Bouhaddou, Mehdi, Anne Marie Barrette, Alan D Stern, Rick J Koch, Matthew S DiStefano, Eric A Riesel, Luis C Santos, Annie L Tan, Alex E Mertz, and Marc R Birtwistle. 2018. “A Mechanistic Pan-Cancer Pathway Model Informed by Multi-Omics Data Interprets Stochastic Cell Fate Responses to Drugs and Mitogens.” PLoS Computational Biology 14 (3). Public Library of Science: e1005985.
Bozic, Ivana, Tibor Antal, Hisashi Ohtsuki, Hannah Carter, Dewey Kim, Sining Chen, Rachel Karchin, Kenneth W Kinzler, Bert Vogelstein, and Martin A Nowak. 2010. “Accumulation of Driver and Passenger Mutations During Tumor Progression.” Proceedings of the National Academy of Sciences 107 (43). National Acad Sciences: 18545–50.
Byrne, Helen M. 2010. “Dissecting Cancer Through Mathematics: From the Cell to the Animal Model.” Nature Reviews Cancer 10 (3). Nature Publishing Group: 221–30.
Calzone, Laurence, Emmanuel Barillot, and Andrei Zinovyev. 2018. “Logical Versus Kinetic Modeling of Biological Networks: Applications in Cancer Research.” Current Opinion in Chemical Engineering 21. Elsevier: 22–31.
Calzone, Laurence, Laurent Tournier, Simon Fourquet, Denis Thieffry, Boris Zhivotovsky, Emmanuel Barillot, and Andrei Zinovyev. 2010. “Mathematical Modelling of Cell-Fate Decision in Response to Death Receptor Engagement.” PLoS Computational Biology 6 (3). Public Library of Science.
De Jong, Hidde. 2002. “Modeling and Simulation of Genetic Regulatory Systems: A Literature Review.” Journal of Computational Biology 9 (1). Mary Ann Liebert, Inc.: 67–103.
Durrett, Richard. 2015. “Branching Process Models of Cancer.” In Branching Process Models of Cancer, 1–63. Springer.
Eberhardt, Frederick, and Richard Scheines. 2007. “Interventions and Causal Inference.” Philosophy of Science 74 (5). The University of Chicago Press: 981–95.
Fey, Dirk, Melinda Halasz, Daniel Dreidax, Sean P Kennedy, Jordan F Hastings, Nora Rauch, Amaya Garcia Munoz, et al. 2015. “Signaling Pathway Models as Biomarkers: Patient-Specific Simulations of Jnk Activity Predict the Survival of Neuroblastoma Patients.” Sci. Signal. 8 (408). American Association for the Advancement of Science: ra130–ra130.
Flobak, Åsmund, Anaïs Baudot, Elisabeth Remy, Liv Thommesen, Denis Thieffry, Martin Kuiper, and Astrid Lægreid. 2015. “Discovery of Drug Synergies in Gastric Cancer Cells Predicted by Logical Modeling.” PLoS Computational Biology 11 (8). Public Library of Science.
Fröhlich, Fabian, Thomas Kessler, Daniel Weindl, Alexey Shadrin, Leonard Schmiester, Hendrik Hache, Artur Muradyan, et al. 2018. “Efficient Parameter Estimation Enables the Prediction of Drug Response Using a Mechanistic Pan-Cancer Pathway Model.” Cell Systems 7 (6). Elsevier: 567–79.
Gupta, Piyush B, Christine M Fillmore, Guozhi Jiang, Sagi D Shapira, Kai Tao, Charlotte Kuperwasser, and Eric S Lander. 2011. “Stochastic State Transitions Give Rise to Phenotypic Equilibrium in Populations of Cancer Cells.” Cell 146 (4). Elsevier: 633–44.
Haeno, Hiroshi, Mithat Gonen, Meghan B Davis, Joseph M Herman, Christine A Iacobuzio-Donahue, and Franziska Michor. 2012. “Computational Modeling of Pancreatic Cancer Reveals Kinetics of Metastasis Suggesting Optimum Treatment Strategies.” Cell 148 (1-2). Elsevier: 362–75.
Hector, Suzanne, Markus Rehm, Jasmin Schmid, Joan Kehoe, Niamh McCawley, Patrick Dicker, Frank Murray, et al. 2012. “Clinical Application of a Systems Model of Apoptosis Execution for the Prediction of Colorectal Cancer Therapy Responses and Personalisation of Therapy.” Gut 61 (5). BMJ Publishing Group: 725–33.
Helikar, Tomáš, John Konvalina, Jack Heidel, and Jim A Rogers. 2008. “Emergent Decision-Making in Biological Signal Transduction Networks.” Proceedings of the National Academy of Sciences 105 (6). National Acad Sciences: 1913–8.
Henry, N Lynn, and Daniel F Hayes. 2012. “Cancer Biomarkers.” Molecular Oncology 6 (2). Wiley Online Library: 140–46.
Hernán, MA, and JM Robins. 2020. “Causal Inference: What If.” Boca Raton: Chapman & Hill/CRC.
Holland, Paul W. 1986. “Statistics and Causal Inference.” Journal of the American Statistical Association 81 (396). Taylor & Francis: 945–60.
Hornberg, Jorrit J, Frank J Bruggeman, Hans V Westerhoff, and Jan Lankelma. 2006. “Cancer: A Systems Biology Disease.” Biosystems 83 (2-3). Elsevier: 81–90.
Jastrzebski, Katarzyna, Bram Thijssen, Roelof JC Kluin, Klaas de Lint, Ian J Majewski, Roderick L Beijersbergen, and Lodewyk FA Wessels. 2018. “Integrative Modeling Identifies Key Determinants of Inhibitor Sensitivity in Breast Cancer Cell Lines.” Cancer Research 78 (15). AACR: 4396–4410.
Kanehisa, Minoru, Susumu Goto, Yoko Sato, Miho Furumichi, and Mao Tanabe. 2012. “KEGG for Integration and Interpretation of Large-Scale Molecular Data Sets.” Nucleic Acids Research 40 (D1). Oxford University Press: D109–D114.
Kauffman, Stuart. 1969. “Homeostasis and Differentiation in Random Genetic Control Networks.” Nature 224 (5215). Springer: 177–78.
Khan, Faiz M, Stephan Marquardt, Shailendra K Gupta, Susanne Knoll, Ulf Schmitz, Alf Spitschak, David Engelmann, Julio Vera, Olaf Wolkenhauer, and Brigitte M Pützer. 2017. “Unraveling a Tumor Type-Specific Regulatory Core Underlying E2f1-Mediated Epithelial-Mesenchymal Transition to Predict Receptor Protein Signatures.” Nature Communications 8 (1). Nature Publishing Group: 1–15.
Kitano, Hiroaki. 2002. “Computational Systems Biology.” Nature 420 (6912). Nature Publishing Group: 206–10.
Knijnenburg, Theo A, Gunnar W Klau, Francesco Iorio, Mathew J Garnett, Ultan McDermott, Ilya Shmulevich, and Lodewyk FA Wessels. 2016. “Logic Models to Predict Continuous Outputs Based on Binary Inputs with an Application to Personalized Cancer Therapy.” Scientific Reports 6 (1). Nature Publishing Group: 1–14.
Knudson, Alfred G. 1971. “Mutation and Cancer: Statistical Study of Retinoblastoma.” Proceedings of the National Academy of Sciences 68 (4). National Acad Sciences: 820–23.
Kreeger, Pamela K, and Douglas A Lauffenburger. 2010. “Cancer Systems Biology: A Network Modeling Perspective.” Carcinogenesis 31 (1). Oxford University Press: 2–8.
Le Novere, Nicolas. 2015. “Quantitative and Logic Modelling of Molecular and Gene Networks.” Nature Reviews Genetics 16 (3). Nature Publishing Group: 146–58.
Letort, Gaelle, Arnau Montagud, Gautier Stoll, Randy Heiland, Emmanuel Barillot, Paul Macklin, Andrei Zinovyev, and Laurence Calzone. 2019. “PhysiBoSS: A Multi-Scale Agent-Based Modelling Framework Integrating Physical Dimension and Cell Signalling.” Bioinformatics 35 (7). Oxford University Press: 1188–96.
Markevich, Nick I, Jan B Hoek, and Boris N Kholodenko. 2004. “Signaling Switches and Bistability Arising from Multisite Phosphorylation in Protein Kinase Cascades.” The Journal of Cell Biology 164 (3). Rockefeller University Press: 353–59.
Murphy, Á C, Birgit Weyhenmeyer, Jasmin Schmid, Seán M Kilbride, Markus Rehm, Heinrich J Huber, C Senft, et al. 2013. “Activation of Executioner Caspases Is a Predictor of Progression-Free Survival in Glioblastoma Patients: A Systems Medicine Approach.” Cell Death & Disease 4 (5). Nature Publishing Group: e629–e629.
Nicolò, Chiara, Cynthia Périer, Melanie Prague, Carine Bellera, Gaëtan MacGrogan, Olivier Saut, and Sébastien Benzekry. 2020. “Machine Learning and Mechanistic Modeling for Prediction of Metastatic Relapse in Early-Stage Breast Cancer.” JCO Clinical Cancer Informatics 4. American Society of Clinical Oncology: 259–74.
Oldenhuis, CNAM, SF Oosting, JA Gietema, and EGE De Vries. 2008. “Prognostic Versus Predictive Value of Biomarkers in Oncology.” European Journal of Cancer 44 (7). Elsevier: 946–53.
Polynikis, Athanasios, SJ Hogan, and Mario di Bernardo. 2009. “Comparing Different Ode Modelling Approaches for Gene Regulatory Networks.” Journal of Theoretical Biology 261 (4). Elsevier: 511–30.
Powathil, Gibin G, Maciej Swat, and Mark AJ Chaplain. 2015. “Systems Oncology: Towards Patient-Specific Treatment Regimes Informed by Multiscale Mathematical Modelling.” In Seminars in Cancer Biology, 30:13–20. Elsevier.
Remy, Elisabeth, Sandra Rebouissou, Claudine Chaouiya, Andrei Zinovyev, François Radvanyi, and Laurence Calzone. 2015. “A Modeling Approach to Explain Mutually Exclusive and Co-Occurring Genetic Alterations in Bladder Tumorigenesis.” Cancer Research 75 (19). AACR: 4042–52.
Saez-Rodriguez, Julio, Leonidas G Alexopoulos, MingSheng Zhang, Melody K Morris, Douglas A Lauffenburger, and Peter K Sorger. 2011a. “Comparing Signaling Networks Between Normal and Transformed Hepatocytes Using Discrete Logical Models.” Cancer Research 71 (16). AACR: 5400–5411.
Salvucci, Manuela, Arman Rahman, Alexa J Resler, Girish M Udupi, Deborah A McNamara, Elaine W Kay, Pierre Laurent-Puig, et al. 2019. “A Machine Learning Platform to Optimize the Translation of Personalized Network Models to the Clinic.” JCO Clinical Cancer Informatics 3. American Society of Clinical Oncology: 1–17.
Salvucci, Manuela, Maximilian L Würstle, Clare Morgan, Sarah Curry, Mattia Cremona, Andreas U Lindner, Orna Bacon, et al. 2017. “A Stepwise Integrated Approach to Personalized Risk Predictions in Stage Iii Colorectal Cancer.” Clinical Cancer Research 23 (5). AACR: 1200–1212.
Salvucci, Manuela, Zaitun Zakaria, Steven Carberry, Amanda Tivnan, Volker Seifert, Donat Kögel, Brona M Murphy, and Jochen HM Prehn. 2019. “System-Based Approaches as Prognostic Tools for Glioblastoma.” BMC Cancer 19 (1). Springer: 1092.
Sawyers, Charles L. 2008. “The Cancer Biomarker Problem.” Nature 452 (7187). Nature Publishing Group: 548–52.
Swanson, Kristin R, Carly Bridge, JD Murray, and Ellsworth C Alvord Jr. 2003. “Virtual and Real Brain Tumors: Using Mathematical Modeling to Quantify Glioma Growth and Invasion.” Journal of the Neurological Sciences 216 (1). Elsevier: 1–10.
Thomas, René. 1973. “Boolean Formalization of Genetic Control Circuits.” Journal of Theoretical Biology 42 (3). Elsevier: 563–85.
Trefois, Christophe, Paul MA Antony, Jorge Goncalves, Alexander Skupin, and Rudi Balling. 2015. “Critical Transitions in Chronic Disease: Transferring Concepts from Ecology to Systems Medicine.” Current Opinion in Biotechnology 34. Elsevier: 48–55.
Tyson, John J, William T Baumann, Chun Chen, Anael Verdugo, Iman Tavassoly, Yue Wang, Louis M Weiner, and Robert Clarke. 2011. “Dynamic Modelling of Oestrogen Signalling and Cell Fate in Breast Cancer Cells.” Nature Reviews Cancer 11 (7). Nature Publishing Group: 523–32.
Tyson, John J, Katherine C Chen, and Bela Novak. 2003. “Sniffers, Buzzers, Toggles and Blinkers: Dynamics of Regulatory and Signaling Pathways in the Cell.” Current Opinion in Cell Biology 15 (2). Elsevier: 221–31.
Villaverde, Alejandro F, and Julio R Banga. 2014. “Reverse Engineering and Identification in Systems Biology: Strategies, Perspectives and Challenges.” Journal of the Royal Society Interface 11 (91). The Royal Society: 20130505.
Wang, Yong, Jill Waters, Marco L Leung, Anna Unruh, Whijae Roh, Xiuqing Shi, Ken Chen, et al. 2014. “Clonal Evolution in Breast Cancer Revealed by Single Nucleus Genome Sequencing.” Nature 512 (7513). Nature Publishing Group: 155–60.
Wittig, Ulrike, Renate Kania, Martin Golebiewski, Maja Rey, Lei Shi, Lenneke Jong, Enkhjargal Algaa, et al. 2012. “SABIO-Rk—database for Biochemical Reaction Kinetics.” Nucleic Acids Research 40 (D1). Oxford University Press: D790–D796.
Zañudo, Jorge Gómez Tejeda, Maurizio Scaltriti, and Réka Albert. 2017. “A Network Modeling Approach to Elucidate Drug Resistance Mechanisms and Predict Combinatorial Drug Treatments in Breast Cancer.” Cancer Convergence 1 (1). Springer: 5.