Chapter 4 Logical modeling principles and data integration

Je suis l’halluciné de la forêt des Nombres.
Ils me fixent, avec leurs yeux de leurs problèmes ;
Ils sont, pour éternellement rester : les mêmes.
Primordiaux et définis,
Ils tiennent le monde entre leurs infinis ;
Ils expliquent le fond et l’essence des choses,
Puisqu’à travers les temps planent leurs causes.
Émile Verhaeren (Les nombres, in Les Flambeaux noirs, 1891)

Another way of ordering the diversity of mechanistic models presented above is to consider their relationship to biological data. Those that make little use of these data are essentially theoretical scope models that describe the general functioning of signaling pathways and associated systems (Calzone et al. 2010). Other models propose more quantitative models but require much more data, either from databases or experimental data generated for this purpose in order to fit the parameters. In the latter case, the necessary data is usually perturbation data: how does my system react to this or that inhibition or activation? For a single cell line this already corresponds to a large amount of data (Razzaq et al. 2018). And if we want to extend these approaches to many cell lines, the amount of data becomes massive (Fröhlich et al. 2018). For patient-specific models, access to this perturbation data is even more difficult.

Between theoretical models that are not very demanding in terms of data but not very applicable clinically and models with a clinical focus but very demanding in terms of data, an intermediate alternative is missing. Can patient-specific mechanistic models be developed that would provide qualitative clinical interpretation with a small amount of data, accessible even in patients? In this part, composed of three chapters, a middle way will be described to answer positively to this question. This methodology will be based on a historically qualitative mathematical formalism already presented in the previous chapter under the name of logical modeling. Logical modeling in general will be detailed in this chapter before describing an original personalized approach in the next two chapters.

Scientific content

This chapter presents the theoretical bases of logical modeling and the tools used thereafter. The content is taken entirely from the literature and the personal presentation that is made is the one that was used to introduce article Béal et al. (2019) and to organize review Béal, Rémy, and Calzone (2020).

4.1 Logical modeling paradigms for qualitative description

Mathematical models serve as tools to answer a biological question in a formal way, to detect blind spots and thus better understand a system, to organize, into a consensual and compact manner, information dispersed in different articles. In the light of this definition, logical formalism may seem one of the closest to natural language in that it can translate quite directly the statements present in the literature such as "protein A activates protein B" or "the expression of gene C requires the joint presence of factors D and E". Indeed, shortly after the first descriptions of control circuits by Jacob and Monod (1961), the interest of logical models to describe biological systems was put forward by Kauffman (1969) and Thomas (1973). Since then, studies have multiplied (Thomas and d’Ari 1990), varying the fields of biological applications and also the mathematical and computational implementations (Naldi, Hernandez, Levy, et al. 2018). The two subsections below summarize the characteristics common to most of the logical formalisms, before detailing the implementation chosen in this thesis in section 4.2. A review of the use of data in logic models will finally be proposed in section 4.3.

4.1.1 Regulatory graph and logical rules

A logical model is based on a network called regulatory graph (Figure 4.1), where each node represents a component (e.g. genes, proteins, complexes, phenotypes or processes), and is associated with discrete levels of activity (\(0\), \(1\), or more when justified). The use of a discrete formalism in molecular network modeling relies on the highly non-linear nature of regulation, and thus on the existence of a regulatory threshold. Assuming that each variable represents a level of expression, it will take the value \(0\) if the level of expression of the entity is below the regulation threshold, i.e., insufficient to carry out the regulation; and the value \(1\) if it is above the threshold and regulation is possible. In other words, the control threshold discretizes the state space, here the expression levels. It is therefore possible to distinguish several thresholds for the same variable, corresponding to distinct controls that do not take place at the same expression levels. The variable is then multivalued. This extension greatly enriches the formalism, because it allows to distinguish situations that are qualitatively different and that would be confused with Boolean variables. In the continuation of this thesis, we will consider by default that the activity levels are binary, \(0\) corresponding to an inactive entity and \(1\) to an active entity. The edges of this regulatory graph correspond to influences, either positive or negative, which illustrate the possible interactions between two entities (Figure 4.1). Positive edges can represent the formation of active complexes, mediation of synthesis, catalysis, etc. and they will be later depicted as green arrows (\(\leftarrow\)). Negative edges on the other hand can represent inhibition of synthesis, degradation, inhibiting (de)phosphorylation, etc. and they will be depicted as red turnstiles (\(\vdash\)).

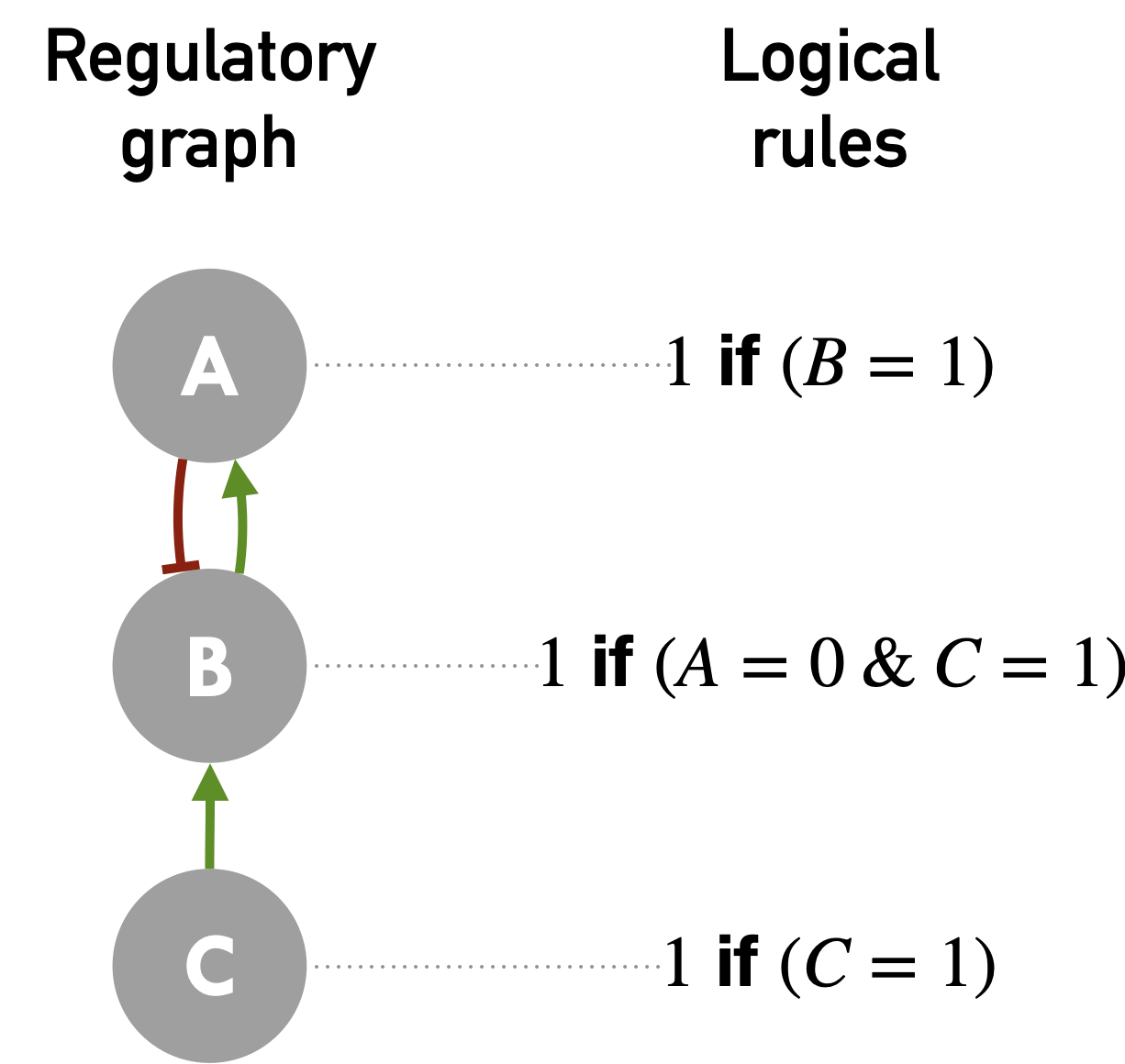
Figure 4.1: A simple example of a logical model. Regulatory graph on the left with positive (green) and negative regulations (red); a set of possible corresponding logical rules on the right.

Then, each node of the regulatory graph has a corresponding Boolean variable associated to it. The variables can take two values: \(0\) for absent or inactive (OFF), and \(1\) for present or active (ON). These variables change their value according to a logical rule assigned to them. The state of a variable will thus depend on its logical rule, which is based on logical statements, i.e., on a function of the node regulators linked with logical connectors AND (\(\&\)), OR (\(|\)) and NOT (\(!\)). These operators can account for what is known about the biology behind these edges. If two input nodes are needed for the activation of the target node, they will be linked by an AND gate; to list different means of activation of a node, an OR gate will be used; and negative influences will rely on NOT gates. The rules corresponding to the toy model in Figure 4.1 could be interpreted literally like this: A is activated to 1 if B is active; B is updated to 1 in the absence of A and the presence/activity of C; C is an input of the model and therefore not regulated. It can be noted that the logical rules cannot be deduced only from the regulatory graph, which is less precise and ambiguous. One could thus imagine that B is activated if C is, OR if A is not, thus changing the behavior of the model.

4.1.2 State transition graph and updates

In a Boolean framework, the variables associated to each node can take two values, either \(0\) or \(1\). We define a model state as a vector of all node states. All the possible transitions from any model state to another are dependent on the set of logical rules that define the model. These transitions can be viewed into a graph called a state transition graph (STG), where nodes are model states and edges are the transitions from one model state to another. STG nodes will be later depicted with rounded squares instead of circles in order to emphasize the difference with regulatory graphs. That way, trajectories from an initial condition to all the final states can be determined. In a model with \(n\) nodes, the STG can contain up to \(2^n\) model state nodes; thus, if \(n\) is too big, the construction and the visualization of the graph become difficult.

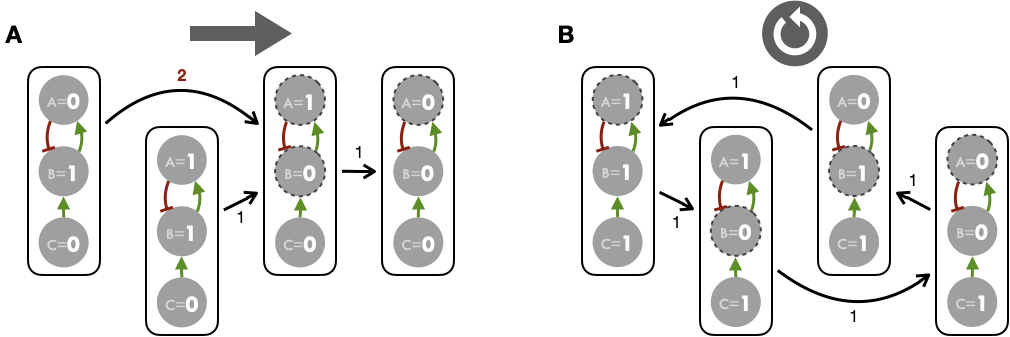
Figure 4.2: State transition graph and synchronous updates. Stable state (A) and limit cycle (B) attractors obtained for the example logical model with synchronous updates (all possible updates simultaneously). Figures above/below STG edges correspond to the number of nodes updated in each transition.

Based the simple logical model of Figure 4.1 it is nevertheless possible to represent the STG comprehensively. The idea for this is to start from a state of the system and track the successive states defined by the logical rules and the corresponding updates. The first strategy to construct this STG is to change simultaneously at each time step all the variables that can be changed (Figure 4.2). This method is referred to as a synchronous updating strategy. In the second method, referred to as a asynchronous updating strategy, variables are changed one at a time (Figure 4.3) and therefore each state has as many successors as there are components whose state must be changed according to logical rules (Figure 4.3A). Performing only one transition at a time implies having to choose this transition between the different possible options, which can be done according to pre-established rules or stochastically as explained in section 4.2. The latter asynchronous method will be used exclusively in the work presented thereafter.

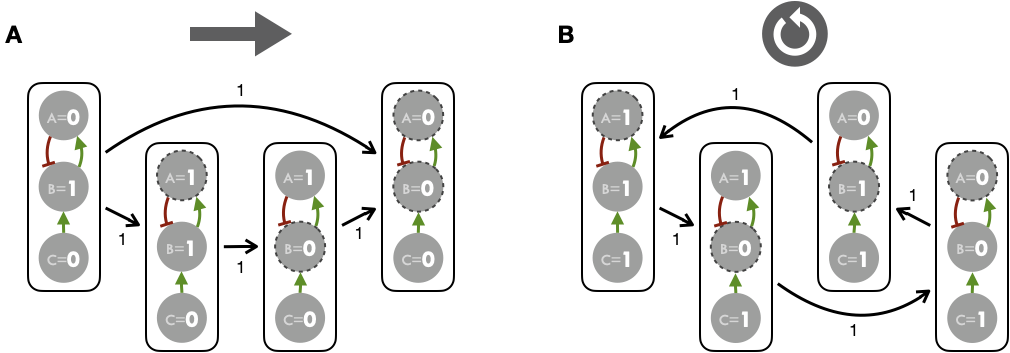
Figure 4.3: State transition graph and asynchronous updates. Stable state (A) and limit cycle (B) attractors obtained for the example logical model with asynchronous updates (one update at a time). Figures above/below STG edges correspond to the number of nodes updated in each transition.

We then define attractors of the model as long-term asymptotic behaviors of the system. Two types of attractors are identified: stable states, when the system has reached a model state whose successor in the transition graph is the model state itself; and cyclic attractors, when trajectories in the transition graph lead to a group of model states that are cycling. For both synchronous and asynchronous updating strategies, the toy model shows the existence of two types of attractors: a stable steady state and a limit cycle, depending on the initial value of \(C\). There are two disconnected components of the STG for this example that correspond to the two possible values for the input \(C\). If \(C\) is initially equal to 0 (inactive), then there exists only one stable state: \(A=B=C=0\). All the trajectories in the state transition graph lead to a single final model state. If \(C\) is initially equal to 1, then the attractor is a limit cycle. The path in the STG cycles for any initial model state of this connected component. Note that for the asynchronous and synchronous graphs, the precise paths or limit cycles may differ. To conclude, it is important to emphasize and illustrate the characteristics of asynchronous updates in this toy example. In Figure 4.3A, the transition from the initial state (\(A=C=0;B=1\)) suggests two distinct possibilities, so it is necessary to define additional rules or heuristics to choose between possible transitions. We will come back to this by specifying the logical modeling implementation chosen in this thesis in section 4.2, in which a stochastic exploration of these alternatives is proposed.

4.1.3 Tools for logical modeling

Numerous tools have been developed to build logical models and study the dynamics of the systems under investigation, each with its own specificity. They allow, for example, to represent regulation networks; to edit, modify or infer logical rules; to identify stable states; to reduce models; to visualize graphs of synchronous or asynchronous transitions. Some also allow to integrate temporal data; to discretize expression data; to simulate the model stochastically or to integrate delays; to identify existing models, etc. Among them, we can cite GINsim (Naldi, Hernandez, Abou-Jaoudé, et al. 2018), BoolNet (Müssel, Hopfensitz, and Kestler 2010), pyBoolNet (Klarner, Streck, and Siebert 2016), BooleanNet (Albert et al. 2008), CellCollective (Helikar et al. 2012), bioLQM (Naldi 2018), MaBoSS (Stoll et al. 2012; Stoll et al. 2017), PINT (Paulevé 2017), CaspoTS (Ostrowski et al. 2016), or CellNOptR (Terfve et al. 2012). The interaction between all these tools, their interoperability and complementarity are highlighted in the form of a notebook Jupyter (Naldi, Hernandez, Levy, et al. 2018), and some of them are described in more details in section 4.3.

4.2 The MaBoSS framework for logical modeling

In the present study, all simulations have been performed with MaBoSS, a Markovian Boolean Stochastic Simulator whose design is summarized in Figure 4.4 and precisely described by Stoll et al. (2012) and Stoll et al. (2017). This framework is based on an asynchronous update scheme combined with a continuous time feature obtained with Gillespie algorithm (Gillespie 1976), allowing simulations to be continuous in time despite the discrete nature of logical modeling.

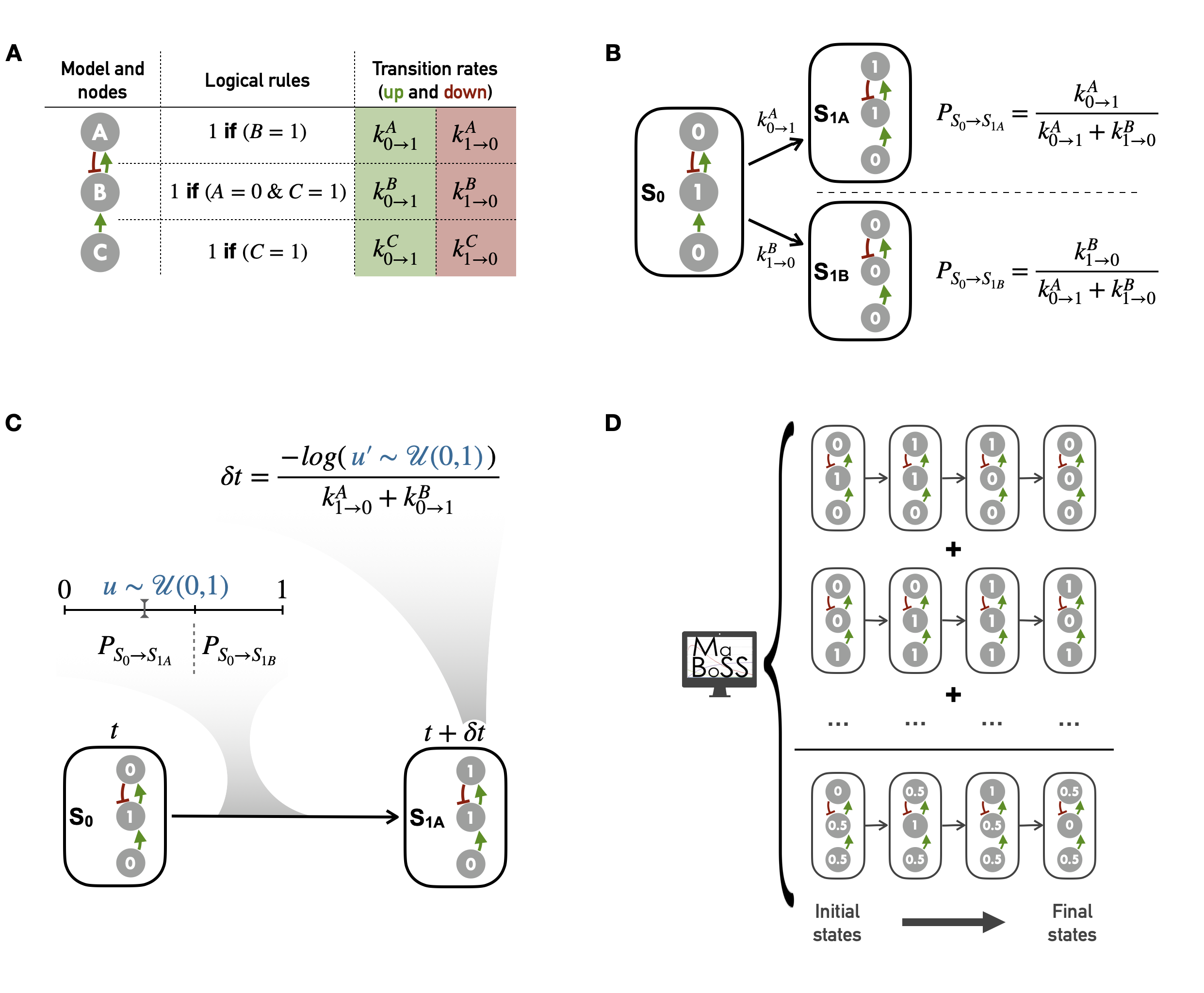
Figure 4.4: Main principles of MaBoSS simulation framework and Gillespie algorithm. (A) A logical model with regulatory graph, logical rules and transition rates. (B) A subset of the corresponding state transition graph with two possible transitions in asynchronous update for a given initial state; the probability probability associated with each transition comes from Gillespie algorithm. (C) Schematic diagram of the Gillespie algorithm applied to the asynchronous transition depicted in (B); random selection of a specific transition and time by the algorithm from two uniform random variables. (D) Schematic representation of a logical model simulation with MaBoSS: average trajectory obtained from the mean of many individual stochastic trajectories, each resulting from the succession of transitions as represented in (C).

4.2.1 Continuous-time Markov processes

The implementation of asynchronous updates proposed by the MaBoSS software is based on continuous time Markov processes applied on a Boolean state space and is therefore part of the large family of stochastic models of cancer outlined in section 3.1. The precise relations of this software with the generic results on Markovian processes, and the associated demonstrations, are available in the original publication by Stoll et al. (2012) and detailed in particular in the related supplementary document⁴. The essence of the formalism, as set out in this article, is outlined below.

Before returning to the simplified example of Figure 4.4, it is possible to describe the general scheme of Markov processes and Gillespie algorithm for simulating logical models. We restrict ourselves here to a Boolean model (binary variables), composed of \(n\) variables. The network state of the system is a vector \(S\) of binary values such as \(S_i \in \{0, 1\}\), with \(i=1,...,n\) and \(S_i\) representing the state of the node \(i\). The network state space of all possible network states is called \(\Omega\). The evolution of the state of the system can be represented by a stochastic process \(s:t \rightarrow s(t)\) defined on \(t \in I \subset \mathbb{R}\) applied on the network state space. For each time \(t \in I \subset \mathbb{R}\), \(s(t)\) represents a random variable applied on the network state space. Thus, \(P[s(t)=S]\in[0, 1], \forall S \in \Omega\) and \(\sum_{S \in \Omega} P[s(t)=S] = 1\). This stochastic process verifies the Markov property which stipulates the absence of memory, i.e., the conditional probability distribution of future states of the process depends only on the present state, not on the sequence of past states. The resulting stochastic process, called Markov process is defined by an initial condition \(P[s(0)=S], \forall S \in \Omega\) and the conditional probabilities \(P[s(t)=S|s(t')=S'], \forall S,S' \in \Omega, \forall t,t' \in I, t'<t\). In this work we will focus on continuous time Markov processes where it has been shown that all conditional probabilities are functions of transition rates \(\rho_{(S' \rightarrow S)} (t) \in [0, \infty[\) (Van Kampen 2004). Only the case of time independent transition rates (and Markov processes) will be explored below.

It is then possible to re-state the description of the logical models in this formalism. One of the first representations of the model is the regulatory network with a set of directed arrows linking the \(n\) nodes (Figure 4.4A, left column). For each node \(i\), a logical rule \(L_i(S)\) is defined based only on the nodes \(j\) for which there exists an arrow from node \(j\) to \(i\), as represented in Figure 4.4A middle column, e.g., \(L_B = (\text{NOT}~A)~\text{AND}~(C)\) with \(L_B\) the logical rule of node \(B\). The notion of asynchronous transition can then be defined as a pair of network states \((S, S') \in \Omega\), written \((S \rightarrow S')\) such that:

\[S'_j=L_B(S) \text{ for a given } j\] \[S'_i=S_i \text{ for } i \neq j\]

This means that during an asynchronous transition, only one node changes state, among those whose logical rule allows it. In Figure 4.4B, two possible asynchronous transitions from the same initial state are represented. Then, transition rates \(\rho_{(S \rightarrow S')}\) are non-zero only if \(S\) and \(S'\) differ by only one node. In that case, each Boolean logic \(L_i(S)\) is replaced by two functions \(k_{0 \rightarrow 1 / 1 \rightarrow 0}^{i}(S) \in [0, \infty[\). The transition rates are defined as follows: if \(i\) is the node that differs from \(S\) and \(S'\), then:

\[\rho_{(S \rightarrow S')}=k_{0 \rightarrow 1}^{i}(S) \text{ if } S_i=0\] \[\rho_{(S \rightarrow S')}=k_{1 \rightarrow 0}^{i}(S) \text{ if } S_i=1\]

Therefore, the continuous Markov process is completely defined by all these \(k^i\) and an initial condition. The state transition graph can also be re-defined as a graph in \(\Omega\), with an edge between \(S\) and \(S'\) if and only if \(\rho_{S \rightarrow S'} > 0\).

4.2.2 Gillespie algorithm

Although the Markov process is completely defined, the cost of its theoretical resolution increases exponentially with the number of nodes since the transition matrix of the system is of size \(2^n \times 2^n\). Thus, although the exact resolution of these Markov processes from their master equation has been well described (Van Kampen 2004), their computational cost quickly becomes too high. As an example, a recent method for the exact resolution of these stochastic processes applied to Boolean models is limited to models of about 20 nodes (Koltai et al. 2020). One solution consists in sampling the probability space by simulating time trajectories in the state transition graph, which is what MaBoSS performs through Gillespie algorithm, also called kinetic Monte-Carlo. The principle of the algorithm is to compute a finite set of individual stochastic trajectories of the Markov process and to use them to infer probabilities for the given Markov process (Figure 4.4D). For the sake of simplicity the remainder of this section will describe the simulation of a single individual stochastic trajectory, first with a focus on the formal description of the algorithm and then with a more qualitative explanation.

A stochastic trajectory \(\hat{S}(t)\) is a function from a predefined time interval \([ 0, t_{max}]\) to \(\Omega\). The iterative computation of the trajectory is obtained as follows:

1. From a state \(S\) at \(t_0\), sum the rates of all possible transitions for leaving this state: \(\rho_{total}=\sum_{S'}{\rho_{(S \rightarrow S')}}\)
2. Draw two uniform random numbers \(u,u' \in [0,1]\)
3. Compute the transition time \(\delta t=-log(u)/\rho_{total}\)
4. Order the potential target states \(S'^{(j)}\) and their corresponding transition rates \(\rho^{(j)}=\rho_{(S \rightarrow S'^{j})}\)
5. Choose the new state \(S'=S'^{(k)}\) such that \(\sum_{j=0}^{k-1} \rho^{(j)} < u'\rho_{total} < \sum_{j=0}^{k} \rho^{(j)}\), with \(\rho^{(0)}=0\)
6. Define the trajectory \(\hat{S}(t)\) such as \(\hat{S}(t)=S\) for \(t \in [t_0, t_0 + \delta t[\) and \(\hat{S}(t_0 + \delta t) = S'\)
7. Repeat iteratively from \(S'\) until \(t_{max}\) is reached

Thus, Gillespie algorithm provides a stochastic way to choose a specific transition among several possible ones and to infer a corresponding time for this transition. To achieve this, transition rates seen as qualitative activation or inactivation rates, must be specified for each node (Figure 4.4A). They can be set either all to the same value by default, in the absence of any indication, or in various levels reflecting different orders of magnitude: post-translational modifications are quicker than transcriptions for instance. These transition rates are translated as transition probabilities in order to determine the actual transition (Figure 4.4B). Indeed, the probability for each possible transition to be chosen for the next update is the ratio of its transition rate to the sum of rates of all possible transitions. Higher rates correspond to transitions that will take place with greater probability, or in other words more quickly. At each update, the Gillespie algorithm performs the procedure described above and depicted schematically in Figure 4.4C. Two uniform random variables \(u\) and \(u'\) are drawn and used respectively to select the transition among the different possibilities (with \(u\)) and to infer the corresponding time (with \(u'\)). Based on the described formula, time \(\delta t\) follows an exponential law whose average is equal to the inverse of the sum of all possible transition rates (Figure 4.4C). In the present work, except otherwise stated, all transition states will be initially assigned to 1.

4.2.3 A stochastic exploration of model behaviours

Since MaBoSS computes stochastic trajectories, it is relevant to compute several trajectories in order to get an insight of the average behavior by generating a population of stochastic trajectories over the asynchronous state transition graph (Figure 4.4D). The aggregation of stochastic trajectories can also be interpreted as a description of a heterogeneous population. Thus, in all the examples in next chapters, all simulations have consisted of thousands of computed trajectories. The larger the model, the larger the space of possibilities and the more trajectories are required to explore it. Since several trajectories are simulated, initial values of each node can be defined with a continuous value between 0 and 1 representing the probability for the node to be defined to 1 for each new trajectory. For instance, a node with a \(0.6\) initial condition will be set to \(1\) in \(60\%\) of simulated trajectories and to \(0\) in \(40\%\) of the cases.

In the present work, we will focus on the asymptotic state of these simulations instead of transient dynamics and we will call node scores the asymptotic agregated score obtained by averaging all trajectories at a given final time point. Indeed, asymptotic states are more closely related to logical model attractors than transient dynamics and are therefore less dependent on updating stochasticity and more biologically meaningful (Huang, Ernberg, and Kauffman 2009). Note that the simulation time should be chosen carefully to ensure that the asymptotic state is achieved, and the term final state may be considered as safer. All in all this modeling framework is at the intersection of logical modeling and continuous dynamic modeling. If the definition of time remains rather abstract and difficult to interpret experimentally, the stochastic exploration of trajectories makes it possible to refine the purely binary interpretation of the variables. Finally, it is important to point out that while the following chapters will focus on the MaBoSS tool, it is not exclusive but on the contrary very complementary to the other logical model analysis tools mentioned in section 4.1.3, or even to the methods specific to Markov processes in particular. The choice of the tools will be made according to the biological questions and the associated analyses: estimation of attractors or basins of attraction, exact resolution, study of transient dynamics, etc.

4.2.4 From theoretical models to data models?

To sum up, logical formalism makes it possible to design qualitative models that reflect a priori knowledge of the phenomena being studied. Thus, they allow answering questions for which there is little quantitative information on the precise mechanisms involved in a disease, for instance a lack of data related to the expression of genes, the quantity of key proteins or the speed of certain processes. Logical models can confirm that a network is a good illustration of the underlying biological question. However, the construction of the model from the literature often results in a generic consensus network that cannot explain the differences observed between certain patients with different molecular profiles. In order to propose a patient-specific mechanistic approach, it seems crucial to use the biological data available. How is this possible in a formalism that is by definition quite abstract?

4.3 Data integration and semi-quantitative logical modeling

The higher level of abstraction of the logical formalism sometimes makes the necessary back and forth between theoretical modeling and experimental or clinical data less easy. However, many theoretical approaches have been developed over the years to enable this dialogue at all stages, from the construction to the validation of a logical model, as summarized in Figure 4.5. This section summarizes some of these approaches to show how the use of biological data enriches logical models and brings them closer to clinical applications in precision medicine. The purpose of this presentation is also to better contextualize the original approach presented in the following chapter. It should be noted that the methods presented below are all applicable to logical models, and illustrated with such examples where possible. However, some methods are not specific to this formalism and can be applied to other modeling frameworks.

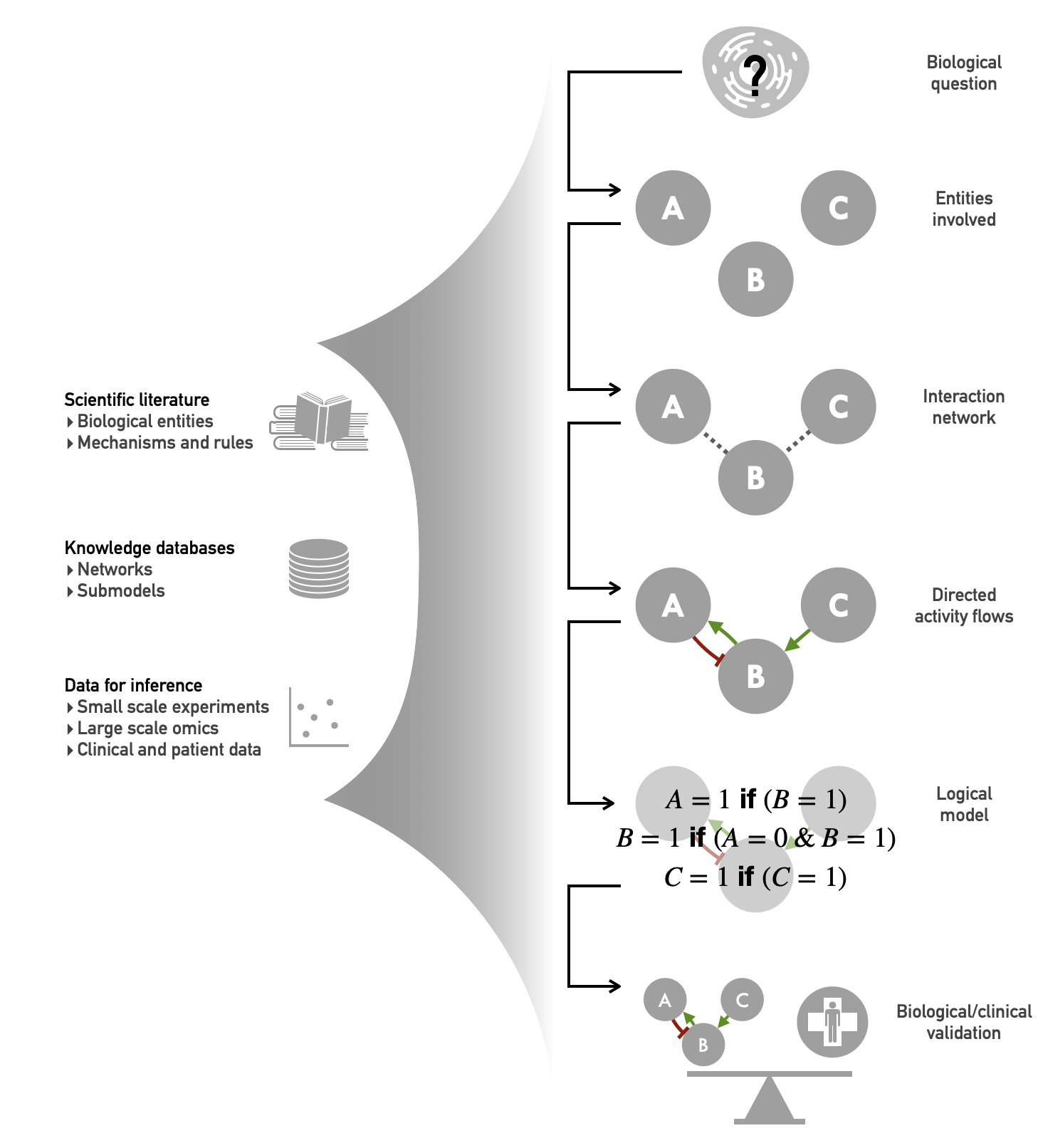
Figure 4.5: Data integration in logical modeling. The main types of data used are shown on the left; the essential steps of the logical modeling are shown linearly on the right.

4.3.1 Build the regulatory graph

Faced with a biological question (Figure 4.5, first step), it is crucial to identify the main actors in the process in order to define the outline of the model (Figure 4.5, second step). A first approach relies on the existing scientific literature on the topic: which biological species and which interactions have been identified as relevant to my problem? In a more automatic way, it is possible to extract information from different databases in order to establish an initial list of biological entities and interactions associated with a biological phenomenon or even a gene of interest (Kanehisa et al. 2012; Perfetto et al. 2016). As an example, starting from the study of E2F1 gene as the hub of many regulatory mechanisms, Khan et al. (2017) have reconstructed a dense network of interactions in the vicinity of E2F1, which will be used for the construction of their subsequent model. The main difficulty here is to choose and select the relevant biological information adapted to the context of the model to be created, depending for example on the type of cancer studied or the desired level of precision.

But if the literature can be considered as processed data, it is also possible to use directly experimental data related to the problem under study. Key actors of biological processes identified by statistical analysis, such as differentially expressed genes or the most frequently mutated genes in a patient cohort, are selected and used as a starting point for the construction of the model (Remy et al. 2015). More comprehensive approaches can use differential analysis tools on signaling pathways, rather than individual genes, to choose the relevant processes to include by contrasting different groups of patients based on their grades, metstatic status, resistance to treatments etc. (Martignetti et al. 2016; Montagud et al. 2017). Similarly, the study of regulatory networks involving transcription factors may justify the use of ChIP-seq data to identify possible new transcriptional regulations not previously listed (Collombet et al. 2017).

Once the main actors have been identified, it is necessary to infer the links between them (Figure 4.5, third and fourth step). However, starting from a list of genes and proteins of interest, how can we ensure that the regulatory relationships are complete and relevant? While a careful reading of the literature can provide locally interesting information, the use of omics data is also a resource that can be broken down into different levels of precision. The major interest of these methods, assuming that the data are adequate and sufficiently massive, is to be able to extract information as large as the dataset, potentially on hundreds of entities, and above all specific to the object of study: a cancer subtype or a particular cell line can thus generate their own interaction network (Lefebvre et al. 2010). Inference methods extract biological knowledge hidden in large databases, summarize it and represent it via networks. Many methods construct coexpression networks, which are non-oriented graphs, with different metrics and methods (Margolin et al. 2006; Vert, Qiu, and Noble 2007). Other approaches seek to infer causal relations between components, allowing the reconstruction of directed graphs where the links between entities are oriented, and sometimes even signed as activating (positive) or inhibiting (negative) regulations. These methods often make use of time series (Hill et al. 2016) or perturbation data (Meinshausen et al. 2016), but also more recently from observational data (Verny et al. 2017). The information extracted from the data is then directly readable in the form of activity flows as described in the SBGN standards (Novère et al. 2009), thus providing a representation adapted to the construction of qualitative models and a fortiori of logical models (Le Novere 2015). Closer to the objective of defining logical models, certain methods allow the study and inference of co-regulation expressed with logical operators (Elati et al. 2007), thus facilitating the passage from the definition of an interaction network to the construction of a true logical model.

4.3.2 Define the logical rules

Precision must then be taken further by defining the logical rules that complete the network (Figure 4.5, fifth step). The first source of aggregated data to define logical rules is the scientific literature. The modeler looks for the state of knowledge on a given regulatory mechanism and translates it into a local logical rule, according to the desired level of precision. For example, it has been observed that the protein kinase AKT can stabilize the oncogene MDM2 by phosphorylation, which leads to the degradation of p53 by forming a complex with it: this example can be translated by a simple inhibition relationship of AKT on p53 if this level of precision is considered sufficient or else intermediate species such as MDM2 can be used (Cohen et al. 2015). Then, the effect of inhibition must be defined: can MDM2 alone inhibit p53 or does the presence of other activators outweigh this effect? This kind of considerations allows to define the logical combinations between the different inputs of a network node. In some cases, experimental data can be used to answer such questions: is a single activator sufficient or is the presence of all activators necessary? Which of the activator or inhibitor prevails in the case of simultaneous presence? While this information is often found in the literature, one should generate one's own experimental data to ensure an answer tailored to the study context, using a variety of experimental molecular biology techniques. For example, in order to elucidate the relationship between Foxo1 and Cebpa in a model of differentiation of myeloid and lymphoid cells, Collombet et al. (2017) first established the physical relationship between these species by ChIP-seq before determining the nature of this relationship using an ectopic expression experiment of Foxo1 in macrophage cells.

Other, more global approaches have been developed in recent years, driven by the influx of data from high-throughput sequencing techniques. Based on this rich and complex data, it has become possible to infer entire logical models, with precisely defined rules and interactions (Ostrowski et al. 2016). The algorithms CellNOpt (Terfve et al. 2012) and caspo (Videla et al. 2017) provide two examples of these approaches, and more recently the SCNS tool described a graphical interface to infer logical models from single cell data (Woodhouse et al. 2018). This model-inference goes beyond simpler structure-inference by defining the logical rules, but it is generally based on a predefined topological structure to which time series or perturbation data are added. These data provide access to the response dynamics of a system. By questioning the way the system reacts, these data are therefore richer than a snapshot and thus facilitate the transition from correlation to causality, and thus the inference of logical rules. In practice, the use of proteomic or phospho-proteomic data is often recommended because these data account for the activity of the protein and are in fact the closest to the cellular response (Ostrowski et al. 2016; Terfve et al. 2012; Terfve et al. 2015). In spite of the richness of this type of data, model inference is sometimes still an under-determined problem that can lead to a large number of models with different logical rules equally compatible with the data. In such situations, it is then a matter of choosing the model on the basis of biological relevance criteria or of accepting to use families of models, or ensemble models, instead of limiting oneself to a single model (Videla et al. 2017). In all cases, constructing logical rules directly from data specific to the problem can make it possible to obtain logical rules that are also specific to the context or the system under study (Saez-Rodriguez, Alexopoulos, et al. 2011b). For example, the inference of logical models specific to one or some cancer cell lines is a powerful tool to study their particularities (Razzaq et al. 2018).

4.3.3 Validate the model

Finally, the data can be used to validate the biological or clinical relevance of the models (Figure 4.5, sixth step). Compared to a system of differential equations, logical modeling has the particularity of being more abstract and therefore less directly reliable to an experimental reality for its validation. A system of differential equations can be compared to the chemical kinetics of the biological system under study. Compared to continuous formalisms, the dynamics of logic model simulation is more difficult to take into account but it is possible to verify it qualitatively, for example by validating the cyclic nature of activation trajectories for a model simulating the cell cycle (Fauré et al. 2006) or cellular decisions as a function of the activation signal (Calzone et al. 2010). A second, more frequent approach consists in looking at the model's steady states and associating them with physiological conditions (Weinstein et al. 2017; Cohen et al. 2015). A third strategy focuses on the asymptotic state reached during the stochastic simulation of the model(s), a state representing a mixture of the different steady states according to the probability that the model has of reaching them. It is also possible, in some model checking frameworks, to study the ability of models to reach certains states, interpreted as cellular types, from given initial conditions (Abou-Jaoudé et al. 2015).

In many models, to facilitate the analysis, nodes representing phenotypes have been added as "read-out" of the activity of certain entities. Thus, if a model includes a node named Proliferation, it will then be simpler to draw interpretations from the simulations performed with the model that will be linked to experimental observations of tumor growth or cell proliferation (Grieco et al. 2013; Steinway et al. 2015). To validate these models, the activity of phenotypes when forcing some node activity to \(0\) or \(1\) is compared with the results of gene mutations reported in experiments carried out on mice or cell lines (Fauré et al. 2006; Cohen et al. 2015). Another similar method for validating the relevance of a logical model is based on the analysis of the effects of different therapeutic molecules. The mechanistic nature of logical modeling makes it possible to simulate the effect of these molecules, at least for targeted treatments with known mechanisms of action. It is then possible to simulate the effect of an inhibitory molecule by forcing the activity of its target to 0 and to compare with data (Zañudo, Scaltriti, and Albert 2017; Iorio et al. 2016; Knijnenburg et al. 2016).

Beyond validation, some studies have predicted new therapeutic targets based on logical models, for instance by pointing out weaknesses in the topology of a regulatory system (Sahin et al. 2009). Taking advantage of the versatility of the formalism to study combinations of therapeutic molecules, logical modeling has also proved fruitful in predicting the best therapeutic combinations and their synergies, in the context of gastric cancers for example (Flobak et al. 2015). Experimental confirmation of the predictions resulting from the modeling is then the ultimate stage in the validation of a logical model, completing the fruitful round trip between models and data.

Summary

Logical models represent a qualitative formalism where biological entities are represented by discrete entities linked together by logical rules. The evolution of the biological system thus modeled can be described as a Markov process, as in the MaBoSS software that stochastically explores the space of possibilities of the model thus defined through a Gillespie algorithm. This approach allows both to avoid the exponential computational cost of exact resolutions and to translate the stochastic diversity of heterogeneous cell populations. Finally, although discrete and theoretical in nature, logical models allow the use of quantitative experimental data, in order to support or validate their biological relevance.

References

Abou-Jaoudé, Wassim, Pedro T Monteiro, Aurélien Naldi, Maximilien Grandclaudon, Vassili Soumelis, Claudine Chaouiya, and Denis Thieffry. 2015. “Model Checking to Assess T-Helper Cell Plasticity.” Frontiers in Bioengineering and Biotechnology 2. Frontiers: 86.

Albert, István, Juilee Thakar, Song Li, Ranran Zhang, and Réka Albert. 2008. “Boolean Network Simulations for Life Scientists.” Source Code for Biology and Medicine 3 (1). BioMed Central: 16.

Béal, Jonas, Arnau Montagud, Pauline Traynard, Emmanuel Barillot, and Laurence Calzone. 2019. “Personalization of Logical Models With Multi-Omics Data Allows Clinical Stratification of Patients.” Frontiers in Physiology. Frontiers Media S.A. doi:10.3389/fphys.2018.01965.

Béal, Jonas, Elizabeth Rémy, and Laurence Calzone. 2020. “Modélisation Logique et Données Omiques : De La Construction Des Modèles à La Médecine Personnalisée.” In Approche Symbolique de La Modélisation et de L’analyse Des Systèmes Biologiques, edited by Elisabeth Rémy and Cédric Lhoussaine. ISTE.

Calzone, Laurence, Laurent Tournier, Simon Fourquet, Denis Thieffry, Boris Zhivotovsky, Emmanuel Barillot, and Andrei Zinovyev. 2010. “Mathematical Modelling of Cell-Fate Decision in Response to Death Receptor Engagement.” PLoS Computational Biology 6 (3). Public Library of Science.

Cohen, David P. A., Loredana Martignetti, Sylvie Robine, Emmanuel Barillot, Andrei Zinovyev, and Laurence Calzone. 2015. “Mathematical Modelling of Molecular Pathways Enabling Tumour Cell Invasion and Migration.” PLOS Computational Biology 11 (11): e1004571. doi:10.1371/journal.pcbi.1004571.

Collombet, Samuel, Chris van Oevelen, Jose Luis Sardina Ortega, Wassim Abou-Jaoude, Bruno Di Stefano, Morgane Thomas-Chollier, Thomas Graf, and Denis Thieffry. 2017. “Logical Modeling of Lymphoid and Myeloid Cell Specification and Transdifferentiation.” Proceedings of the National Academy of Sciences 114 (23): 5792–9. doi:10.1073/pnas.1610622114.

Elati, Mohamed, Pierre Neuvial, Monique Bolotin-Fukuhara, Emmanuel Barillot, François Radvanyi, and Céline Rouveirol. 2007. “LICORN: Learning Cooperative Regulation Networks from Gene Expression Data.” Bioinformatics 23 (18): 2407–14. doi:10.1093/bioinformatics/btm352.

Fauré, Adrien, Aurélien Naldi, Claudine Chaouiya, and Denis Thieffry. 2006. “Dynamical Analysis of a Generic Boolean Model for the Control of the Mammalian Cell Cycle.” Bioinformatics 22 (14). Oxford University Press: e124–e131.

Flobak, Åsmund, Anaïs Baudot, Elisabeth Remy, Liv Thommesen, Denis Thieffry, Martin Kuiper, and Astrid Lægreid. 2015. “Discovery of Drug Synergies in Gastric Cancer Cells Predicted by Logical Modeling.” PLoS Computational Biology 11 (8). Public Library of Science.

Fröhlich, Fabian, Thomas Kessler, Daniel Weindl, Alexey Shadrin, Leonard Schmiester, Hendrik Hache, Artur Muradyan, et al. 2018. “Efficient Parameter Estimation Enables the Prediction of Drug Response Using a Mechanistic Pan-Cancer Pathway Model.” Cell Systems 7 (6). Elsevier: 567–79.

Gillespie, Daniel T. 1976. “A General Method for Numerically Simulating the Stochastic Time Evolution of Coupled Chemical Reactions.” Journal of Computational Physics 22 (4): 403–34. doi:10.1016/0021-9991(76)90041-3.

Grieco, Luca, Laurence Calzone, Isabelle Bernard-Pierrot, François Radvanyi, Brigitte Kahn-Perles, and Denis Thieffry. 2013. “Integrative Modelling of the Influence of Mapk Network on Cancer Cell Fate Decision.” PLoS Computational Biology 9 (10). Public Library of Science: e1003286.

Helikar, Tomáš, Bryan Kowal, Sean McClenathan, Mitchell Bruckner, Thaine Rowley, Alex Madrahimov, Ben Wicks, Manish Shrestha, Kahani Limbu, and Jim A Rogers. 2012. “The Cell Collective: Toward an Open and Collaborative Approach to Systems Biology.” BMC Systems Biology 6 (1). BioMed Central: 96.

Hill, Steven M, Laura M Heiser, Thomas Cokelaer, Michael Unger, Nicole K Nesser, Daniel E Carlin, Yang Zhang, et al. 2016. “Inferring Causal Molecular Networks: Empirical Assessment Through a Community-Based Effort.” Nature Methods 13 (4). Nature Publishing Group: 310.

Huang, Sui, Ingemar Ernberg, and Stuart Kauffman. 2009. “Cancer Attractors: A Systems View of Tumors from a Gene Network Dynamics and Developmental Perspective” 20 (7). Elsevier: 869–76.

Iorio, Francesco, Theo A Knijnenburg, Daniel J Vis, Graham R Bignell, Michael P Menden, Michael Schubert, Nanne Aben, et al. 2016. “A Landscape of Pharmacogenomic Interactions in Cancer.” Cell 166 (3). Elsevier: 740–54.

Jacob, François, and Jacques Monod. 1961. “Genetic Regulatory Mechanisms in the Synthesis of Proteins.” Journal of Molecular Biology 3 (3). Elsevier: 318–56.

Kanehisa, Minoru, Susumu Goto, Yoko Sato, Miho Furumichi, and Mao Tanabe. 2012. “KEGG for Integration and Interpretation of Large-Scale Molecular Data Sets.” Nucleic Acids Research 40 (D1). Oxford University Press: D109–D114.

Kauffman, Stuart. 1969. “Homeostasis and Differentiation in Random Genetic Control Networks.” Nature 224 (5215). Springer: 177–78.

Khan, Faiz M, Stephan Marquardt, Shailendra K Gupta, Susanne Knoll, Ulf Schmitz, Alf Spitschak, David Engelmann, Julio Vera, Olaf Wolkenhauer, and Brigitte M Pützer. 2017. “Unraveling a Tumor Type-Specific Regulatory Core Underlying E2f1-Mediated Epithelial-Mesenchymal Transition to Predict Receptor Protein Signatures.” Nature Communications 8 (1). Nature Publishing Group: 1–15.

Klarner, Hannes, Adam Streck, and Heike Siebert. 2016. “PyBoolNet: A Python Package for the Generation, Analysis and Visualization of Boolean Networks.” Bioinformatics 33 (5). Oxford University Press: 770–72.

Knijnenburg, Theo A, Gunnar W Klau, Francesco Iorio, Mathew J Garnett, Ultan McDermott, Ilya Shmulevich, and Lodewyk FA Wessels. 2016. “Logic Models to Predict Continuous Outputs Based on Binary Inputs with an Application to Personalized Cancer Therapy.” Scientific Reports 6 (1). Nature Publishing Group: 1–14.

Koltai, Mihály, Vincent Noel, Andrei Zinovyev, Laurence Calzone, and Emmanuel Barillot. 2020. “Exact Solving and Sensitivity Analysis of Stochastic Continuous Time Boolean Models.” BMC Bioinformatics 21 (1). Springer: 1–22.

Le Novere, Nicolas. 2015. “Quantitative and Logic Modelling of Molecular and Gene Networks.” Nature Reviews Genetics 16 (3). Nature Publishing Group: 146–58.

Lefebvre, Celine, Presha Rajbhandari, Mariano J. Alvarez, Pradeep Bandaru, Wei Keat Lim, Mai Sato, Kai Wang, et al. 2010. “A Human B-Cell Interactome Identifies MYB and FOXM1 as Master Regulators of Proliferation in Germinal Centers.” Molecular Systems Biology 6 (June): 377. doi:10.1038/msb.2010.31.

Margolin, Adam A., Ilya Nemenman, Katia Basso, Chris Wiggins, Gustavo Stolovitzky, Riccardo Dalla Favera, and Andrea Califano. 2006. “ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context.” BMC Bioinformatics 7 (1): S7. doi:10.1186/1471-2105-7-S1-S7.

Martignetti, Loredana, Laurence Calzone, Eric Bonnet, Emmanuel Barillot, and Andrei Zinovyev. 2016. “ROMA: Representation and Quantification of Module Activity from Target Expression Data.” Frontiers in Genetics 7. Frontiers: 18.

Meinshausen, Nicolai, Alain Hauser, Joris M Mooij, Jonas Peters, Philip Versteeg, and Peter Bühlmann. 2016. “Methods for Causal Inference from Gene Perturbation Experiments and Validation.” Proceedings of the National Academy of Sciences 113 (27). National Acad Sciences: 7361–8.

Montagud, Arnau, Pauline Traynard, Loredana Martignetti, Eric Bonnet, Emmanuel Barillot, Andrei Zinovyev, and Laurence Calzone. 2017. “Conceptual and Computational Framework for Logical Modelling of Biological Networks Deregulated in Diseases.” Briefings in Bioinformatics. doi:10.1093/bib/bbx163.

Müssel, Christoph, Martin Hopfensitz, and Hans A Kestler. 2010. “BoolNet?an R Package for Generation, Reconstruction and Analysis of Boolean Networks.” Bioinformatics 26 (10). Oxford University Press: 1378–80.

Naldi, Aurélien. 2018. “BioLQM: A Java Toolkit for the Manipulation and Conversion of Logical Qualitative Models of Biological Networks.” Frontiers in Physiology 9. Frontiers: 1605.

Naldi, Aurélien, Céline Hernandez, Wassim Abou-Jaoudé, Pedro T Monteiro, Claudine Chaouiya, and Denis Thieffry. 2018. “Logical Modeling and Analysis of Cellular Regulatory Networks with Ginsim 3.0.” Frontiers in Physiology 9. Frontiers Media SA.

Naldi, Aurélien, Céline Hernandez, Nicolas Levy, Gautier Stoll, Pedro T Monteiro, Claudine Chaouiya, Tomáš Helikar, et al. 2018. “The Colomoto Interactive Notebook: Accessible and Reproducible Computational Analyses for Qualitative Biological Networks.” Frontiers in Physiology 9. Frontiers: 680.

Novère, Nicolas Le, Michael Hucka, Huaiyu Mi, Stuart Moodie, Falk Schreiber, Anatoly Sorokin, Emek Demir, et al. 2009. “The Systems Biology Graphical Notation.” Nature Biotechnology 27 (8): 735–41. doi:10.1038/nbt.1558.

Ostrowski, M., L. Paulevé, T. Schaub, A. Siegel, and C. Guziolowski. 2016. “Boolean Network Identification from Perturbation Time Series Data Combining Dynamics Abstraction and Logic Programming.” Biosystems, Selected papers from the Computational Methods in Systems Biology 2015 conference, 149 (November): 139–53. doi:10.1016/j.biosystems.2016.07.009.

Paulevé, Loïc. 2017. “Pint: A Static Analyzer for Transient Dynamics of Qualitative Networks with IPython Interface.” In CMSB 2017 - 15th conference on Computational Methods for Systems Biology, 10545:370–16. Lecture Notes in Computer Science. Springer. doi:10.1007/978-3-319-67471-1\_20.

Perfetto, Livia, Leonardo Briganti, Alberto Calderone, Andrea Cerquone Perpetuini, Marta Iannuccelli, Francesca Langone, Luana Licata, et al. 2016. “SIGNOR: A Database of Causal Relationships Between Biological Entities.” Nucleic Acids Research 44 (D1). Oxford University Press: D548–D554.

Razzaq, Misbah, Loïc Paulevé, Anne Siegel, Julio Saez-Rodriguez, Jérémie Bourdon, and Carito Guziolowski. 2018. “Computational Discovery of Dynamic Cell Line Specific Boolean Networks from Multiplex Time-Course Data.” PLoS Computational Biology 14 (10). Public Library of Science: e1006538.

Remy, Elisabeth, Sandra Rebouissou, Claudine Chaouiya, Andrei Zinovyev, François Radvanyi, and Laurence Calzone. 2015. “A Modeling Approach to Explain Mutually Exclusive and Co-Occurring Genetic Alterations in Bladder Tumorigenesis.” Cancer Research 75 (19). AACR: 4042–52.

Saez-Rodriguez, Julio, Leonidas G. Alexopoulos, MingSheng Zhang, Melody K. Morris, Douglas A. Lauffenburger, and Peter K. Sorger. 2011b. “Comparing Signaling Networks Between Normal and Transformed Hepatocytes Using Discrete Logical Models.” Cancer Research 71 (16): 5400–5411. doi:10.1158/0008-5472.CAN-10-4453.

Sahin, Özgür, Holger Fröhlich, Christian Löbke, Ulrike Korf, Sara Burmester, Meher Majety, Jens Mattern, et al. 2009. “Modeling Erbb Receptor-Regulated G1/S Transition to Find Novel Targets for de Novo Trastuzumab Resistance.” BMC Systems Biology 3 (1). BioMed Central: 1.

Steinway, Steven Nathaniel, Jorge Gomez Tejeda Zañudo, Paul J Michel, David J Feith, Thomas P Loughran, and Reka Albert. 2015. “Combinatorial Interventions Inhibit Tgf\(\beta\)-Driven Epithelial-to-Mesenchymal Transition and Support Hybrid Cellular Phenotypes.” NPJ Systems Biology and Applications 1. Nature Publishing Group: 15014.

Stoll, Gautier, Barthélémy Caron, Eric Viara, Aurélien Dugourd, Andrei Zinovyev, Aurélien Naldi, Guido Kroemer, Emmanuel Barillot, and Laurence Calzone. 2017. “MaBoSS 2.0: An Environment for Stochastic Boolean Modeling.” Bioinformatics 33 (14). Oxford University Press: 2226–8.

Stoll, Gautier, Eric Viara, Emmanuel Barillot, and Laurence Calzone. 2012. “Continuous Time Boolean Modeling for Biological Signaling: Application of Gillespie Algorithm.” BMC Systems Biology 6 (1). BioMed Central: 116.

Terfve, Camille D. A., Edmund H. Wilkes, Pedro Casado, Pedro R. Cutillas, and Julio Saez-Rodriguez. 2015. “Large-Scale Models of Signal Propagation in Human Cells Derived from Discovery Phosphoproteomic Data.” Nature Communications 6 (September): 8033. doi:10.1038/ncomms9033.

Terfve, Camille, Thomas Cokelaer, David Henriques, Aidan MacNamara, Emanuel Goncalves, Melody K. Morris, Martijn van Iersel, Douglas A. Lauffenburger, and Julio Saez-Rodriguez. 2012. “CellNOptR: A Flexible Toolkit to Train Protein Signaling Networks to Data Using Multiple Logic Formalisms.” BMC Systems Biology 6 (1): 133. doi:10.1186/1752-0509-6-133.

Thomas, René. 1973. “Boolean Formalization of Genetic Control Circuits.” Journal of Theoretical Biology 42 (3). Elsevier: 563–85.

Thomas, René, and Richard d’Ari. 1990. Biological Feedback. CRC press.

Van Kampen, NG. 2004. “Stochastic Processes in Physics and Chemistry. 5th.” Elsevier Amsterdam:

Verny, Louis, Nadir Sella, Séverine Affeldt, Param Priya Singh, and Hervé Isambert. 2017. “Learning Causal Networks with Latent Variables from Multivariate Information in Genomic Data.” PLOS Computational Biology 13 (10): e1005662. doi:10.1371/journal.pcbi.1005662.

Vert, Jean-Philippe, Jian Qiu, and William S. Noble. 2007. “A New Pairwise Kernel for Biological Network Inference with Support Vector Machines.” BMC Bioinformatics 8 (Suppl 10): S8.

Videla, Santiago, Julio Saez-Rodriguez, Carito Guziolowski, and Anne Siegel. 2017. “Caspo: A Toolbox for Automated Reasoning on the Response of Logical Signaling Networks Families.” Bioinformatics 33 (6): 947–50. doi:10.1093/bioinformatics/btw738.

Weinstein, Nathan, Luis Mendoza, Isidoro Gitler, and Jaime Klapp. 2017. “A Network Model to Explore the Effect of the Micro-Environment on Endothelial Cell Behavior During Angiogenesis.” Frontiers in Physiology 8. Frontiers: 960.

Woodhouse, Steven, Nir Piterman, Christoph M Wintersteiger, Berthold Göttgens, and Jasmin Fisher. 2018. “SCNS: A Graphical Tool for Reconstructing Executable Regulatory Networks from Single-Cell Genomic Data.” BMC Systems Biology 12 (1). BioMed Central: 59.

Zañudo, Jorge Gómez Tejeda, Maurizio Scaltriti, and Réka Albert. 2017. “A Network Modeling Approach to Elucidate Drug Resistance Mechanisms and Predict Combinatorial Drug Treatments in Breast Cancer.” Cancer Convergence 1 (1). Springer: 5.

---

4. Additional information on Markov processes and MaBoSS in the following document↩